简介
在之前的博客中 (Ceres 学习记录(一)),我结合 2D 激光 SLAM 简单介绍了一下应用 Ceres Solver 的基本用法,这篇博客主要是在 3D 激光 SLAM 框架中基于 Ceres Solver 实现激光里程计,GNSS 以及回环约束在 KITTI 数据集下进行图优化。
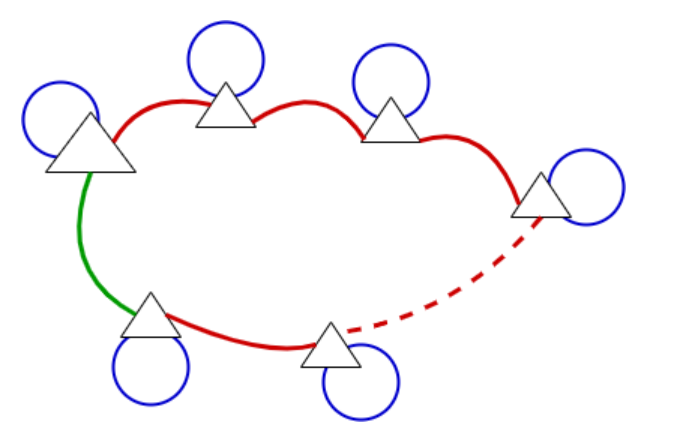
简单介绍了一下优化过程中涉及的节点和边。首先是节点,由于是纯激光 SLAM (没有 IMU 和视觉等),因此优化变量只有载体的位姿。因此这个图也是个位姿图。边包括三种:激光里程计产生的前后两帧的相对位姿约束,GNSS 对位姿节点的先验约束以及回环检测产生的轨迹中形成回环的两帧的相对位姿约束。如下图所示,三角形为载体位姿,红边为激光里程计对相邻两帧的位姿约束,蓝边为 GNSS 对某一帧的的位置约束(不包含姿态),绿边为回环检测到的某两帧之间的位姿约束。
关于非线性优化的原理可以参考:最小二乘问题和非线性优化。在这个问题中,图优化需要做到以下几步:
- 添加节点(位姿)和边(位姿或位置约素)为优化做准备
- 优化过程,对每条边计算误差以及对优化变量的雅可比矩阵,这里的边有两个类型(两帧节点之间的相对位姿观测,以及对单个节点的位置观测),我们需要对这两种边的误差以及雅可比计算方式进行推导
- 选择合适的优化策略,如 LM 或者 Dogleg 法,利用每个观测的误差和雅可比矩阵构建正规方程
$\boldsymbol{H}\Delta\boldsymbol{x} = \boldsymbol{b}$ - 对上述方程选择合适的方式进行求解,例如 QR 分解、Cholesky 分解等
- 按照需要添加鲁棒核函数,不过这里基本都是位姿之间的约束,不涉及特征,因此误匹配的情况应该比较少
接下来看 Ceres 如何实现上述过程。
节点和边的定义
节点的定义很简单,每个节点代表一个位姿,包含相对于全局坐标系的平移部分和旋转部分。定义如下所示,这里旋转部分我们用四元数表示,是过参数化的,因此在优化中需要给 ceres 提供旋转部分的参数化方法(如何对其进行更新),这一部分后面会介绍:
struct PoseSE3 {
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
Eigen::Vector3d pos = Eigen::Vector3d::Zero();
Eigen::Quaterniond quat = Eigen::Quaterniond::Identity();
};
姿态的参数化
由于上面我们使用了四元数来作为姿态的存储方式,而四元数只有三个自由度,是过参数化的,因此最后通过求解正规方程得到的(三维)迭代量不能直接加在四元数上,我们需要定义四元数的参数化,来告诉 Ceres Solver 怎么对其进行更新。Ceres 已经提供了对 Eigen::Quaternion 类型的参数化类 EigenQuaternionParameterization。下面借助这个类来对 Ceres 如何处理过参数化的变量的更新迭代。
class CERES_EXPORT EigenQuaternionParameterization
: public ceres::LocalParameterization {
public:
virtual ~EigenQuaternionParameterization() {}
bool Plus(const double* x,
const double* delta,
double* x_plus_delta) const override;
bool ComputeJacobian(const double* x, double* jacobian) const override;
int GlobalSize() const override { return 4; }
int LocalSize() const override { return 3; }
};
上述代码中,ceres::LocalParameterization 为抽象类,EigenQuaternionParameterization 需要实现抽象类中定义的四个函数,分别为:
GlobalSize()返回变量维度,对于四元数而言维度为 4LocalSize()返回变量的自由度(在正切空间的维度),对于四元数而言为 3bool Plus(const double* x, const double* delta, double* x_plus_delta):给定一个更新量(维度为LocalSize())如何对该参数进行更新bool ComputeJacobian(const double* x, double* jacobian):计算该参数加上更新量的结果对更新量的雅可比矩阵
下面主要分析 bool Plus() 和 bool ComputeJacobian() 这两个函数。
先整理一下对过参数化变量迭代的过程。主要包括误差计算,雅可比求解以及构建正规方程求解迭代量,最后对待优化变量进行求解。以四元数为例,四元数本身的维度是 4,但其自由度只有 3,因此迭代量的维度也应该是 3,因此如果直接在求观测误差对四元数求雅可比时,得到的结果维度和该变量的维度是一致的,这样的问题是其同样具有冗余的自由度,因此还需要对其迭代量进行雅可比求解,整体的过程可以用下式来表示:
$$
\begin{aligned}
\boldsymbol{J} &= \frac{\partial\boldsymbol{e}}{\partial\Delta\boldsymbol{x}}\\
&= \frac{\partial\boldsymbol{e}}{\partial\boldsymbol{x}}\frac{\partial(\boldsymbol{x}\boxplus\Delta\boldsymbol{x})}{\partial\Delta\boldsymbol{x}}
\end{aligned}
$$
在四元数上的例子则是,下式中 $\boldsymbol{q}$ 为四元数,维度为 4,$\Delta\boldsymbol{\theta}$ 为作用在四元数上的更新量,维度为 3:
$$
\begin{aligned}
\boldsymbol{J} &= \frac{\partial\boldsymbol{e}}{\partial\boldsymbol{q}}\frac{\partial(\boldsymbol{q}\boxplus\Delta\boldsymbol{\theta})}{\partial\Delta\boldsymbol{\theta}}\\
\end{aligned}
$$
第一部分通常会在观测边(即残差部分)上定义,方式可以通过自动求导或者解析求导获得,列数和待优化变量一致。这里假设误差维度为 3,那么求解的雅可比的维度应该是 3x4。因此对于待优化参数块,我们还需要实现两个函数,即待优化变量对迭代量的求导,以及给定迭代量对待优化变量的迭代方式(即式中的广义加法 $\boxplus$)分别对应 ceres::LocalParameterization 中的 ComputeJacobian() 和 Plus()。接下来看一下 Ceres 提供的 EigenQuaternionParameterization 是如何实现的。
先看广义加法,即对待优化四元数进行更新:
bool EigenQuaternionParameterization::Plus(const double* x_ptr,
const double* delta,
double* x_plus_delta_ptr) const {
Eigen::Map<Eigen::Quaterniond> x_plus_delta(x_plus_delta_ptr);
Eigen::Map<const Eigen::Quaterniond> x(x_ptr);
const double norm_delta =
sqrt(delta[0] * delta[0] + delta[1] * delta[1] + delta[2] * delta[2]);
if (norm_delta > 0.0) {
const double sin_delta_by_delta = sin(norm_delta) / norm_delta;
// Note, in the constructor w is first.
Eigen::Quaterniond delta_q(cos(norm_delta),
sin_delta_by_delta * delta[0],
sin_delta_by_delta * delta[1],
sin_delta_by_delta * delta[2]);
x_plus_delta = delta_q * x;
} else {
x_plus_delta = x;
}
return true;
}
函数中获得的迭代量为旋转向量,因此需要通过旋转向量构造四元数,方法也很简单,利用以下公式即可,假设旋转向量为 $\boldsymbol{n} = \theta\boldsymbol{u}$,最后这里更新四元数用的是迭代量左乘,这里 Plus 接收的迭代量本来就是半轴角,所以没有除以 2:
$$
\boldsymbol{q} = \begin{bmatrix}
\cos(\theta/2)\\
\boldsymbol{u}\sin(\theta/2)
\end{bmatrix}
$$
接下来看雅可比计算函数,对这个雅可比进行维度分析,四元数维度为 4,迭代量维度为 3,因此雅可比维度应该是 4x3:
bool EigenQuaternionParameterization::ComputeJacobian(const double* x,
double* jacobian) const {
// clang-format off
jacobian[0] = x[3]; jacobian[1] = x[2]; jacobian[2] = -x[1];
jacobian[3] = -x[2]; jacobian[4] = x[3]; jacobian[5] = x[0];
jacobian[6] = x[1]; jacobian[7] = -x[0]; jacobian[8] = x[3];
jacobian[9] = -x[0]; jacobian[10] = -x[1]; jacobian[11] = -x[2];
// clang-format on
return true;
}
咋一看可能有点云里雾里,接下来进行推导,Ceres 通常采用的内存布局为 w, x, y, z,下面基于这个假设进行推导,由于广义加法定义的是迭代量左乘,因此这里也要用左乘:
$$
\begin{aligned}
\boldsymbol{J} &= \frac{\partial\boldsymbol{q}\boxplus\Delta\boldsymbol{x}}{\Delta\boldsymbol{x}} \\
&\approx \frac{\partial(
\begin{bmatrix}
1 \\ \Delta\boldsymbol{x}
\end{bmatrix}\otimes\boldsymbol{q}
)}{\partial\Delta\boldsymbol{x}}\\
&=\frac{\partial[\boldsymbol{q}]_R
\begin{bmatrix}
1 \\ \Delta\boldsymbol{x}
\end{bmatrix}}{\partial\Delta\boldsymbol{x}}\\
&= [\boldsymbol{q}]_R
\frac{\partial
\begin{bmatrix}
1 \\ \Delta\boldsymbol{x}
\end{bmatrix}}{\partial\Delta\boldsymbol{x}}\\
&= [\boldsymbol{q}]_R
\begin{bmatrix}
\boldsymbol{0}\\
\boldsymbol{I}
\end{bmatrix}\\
&=
\begin{bmatrix}
q_w & -q_x & -q_y & -q_z\\
q_x & q_w & q_z & -q_y\\
q_y & -q_z & q_w & q_x\\
q_z & q_y & -q_x & q_w
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{0}\\
\boldsymbol{I}
\end{bmatrix}\\
&=
\begin{bmatrix}
-q_x & -q_y & -q_z\\
q_w & q_z & -q_y\\
-q_z & q_w & q_x\\
q_y & -q_x & q_w
\end{bmatrix}
\end{aligned}
$$
和代码对应一下,代码接收的四元数为 Eigen::Quaternion,其内部内存分布为:x, y, z, w 和 Ceres 存储的顺序不同 (w, x, y, z)因此,x[0], x[1], x[2], x[3] 分别对应 x, y, z, w,因此求导结果需要进行调整如下,将第一行放在最后一行:
$$
\begin{aligned}
\boldsymbol{J} &=
\begin{bmatrix}
q_w & q_z & -q_y\\
-q_z & q_w & q_x\\
q_y & -q_x & q_w\\
-q_x & -q_y & -q_z
\end{bmatrix}
\end{aligned}
$$
结果和代码一致。
注意:在实际使用时,我们经常不会这么先对过参数化的变量求导,例如在使用旋转矩阵表示时,常见的做法是直接利用左/右扰动模型来求导,此时 ComputeJacobian 的意义不是将过参数化变量对迭代量求导,而只是将上一部分的雅可比进行一定转化获得正确维度的结果而已。可以参考:ceres_R_LocalParam, FLOAM
对位置的观测边
接下来看看边,主要有两个:对位置的观测边以及对两帧位姿的观测边。Ceres 提供了两种定义边方式,一种使用自动求导,不用自己写雅可比矩阵计算方式,另一种方式需要用户提供雅可比实现。这里先看一下不包含雅可比的实现方式:
class PriorPositionEdge {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
PriorPositionEdge(const Eigen::Vector3d& measurement, const Eigen::Matrix3d& sqrt_info)
: measurement_(measurement), sqrt_info_(sqrt_info) {}
template <typename T>
bool operator()(const T* const v1, T* residual) const {
Eigen::Map<const Eigen::Matrix<T, 3, 1>> estimate(v1);
Eigen::Map<Eigen::Matrix<T, 3, 1>> residual_eigen(residual);
residual_eigen = estimate - measurement_;
residual_eigen.applyOnTheLeft(sqrt_info_.template cast<T>());
return true;
}
static ceres::CostFunction* create(const Eigen::Vector3d& measurement, const Eigen::Matrix3d& sqrt_info) {
return (
new ceres::AutoDiffCostFunction<PriorPositionEdge, 3, 3>(new PriorPositionEdge(measurement, sqrt_info)));
}
private:
Eigen::Vector3d measurement_;
Eigen::Matrix3d sqrt_info_;
};
可以看到,整体来说这个观测边还是比较简单,本身观测也是一个位置量,因此计算误差方式为直接和对应的节点位置相减。选择自动求导的方式需要重载 operator() 作为函数模版。因此在函数里面使用 Eigen 时要注意不要使用特定类型,且由于函数接收的是指针,因此在使用 Eigen 进行 Map 时需要注意维度。这里注意一下,由于 Ceres 本身是作为一个通用的非线性最小二乘优化库,因此对约束没有额外的添加信息矩阵的接口。我们可以将信息矩阵融入进误差计算过程,如下所示:
$$
\begin{aligned}
\boldsymbol{H}\Delta\boldsymbol{x} &= \boldsymbol{b}\\
\boldsymbol{J}^T\boldsymbol{\Lambda}\boldsymbol{J}\Delta\boldsymbol{x} &= -\boldsymbol{J}^T\boldsymbol{\Lambda}\boldsymbol{e}\\
\boldsymbol{J}^T(\boldsymbol{\Lambda}^{1/2})(\boldsymbol{\Lambda}^{1/2})\boldsymbol{J}\Delta\boldsymbol{x} &= -\boldsymbol{J}^T(\boldsymbol{\Lambda}^{1/2})(\boldsymbol{\Lambda}^{1/2})\boldsymbol{e}\\
(\boldsymbol{\Lambda}^{1/2}\boldsymbol{J})^T(\boldsymbol{\Lambda}^{1/2}\boldsymbol{J})\Delta\boldsymbol{x} &= -(\boldsymbol{\Lambda}^{1/2}\boldsymbol{J})^T(\boldsymbol{\Lambda}^{1/2}\boldsymbol{e})\\
\boldsymbol{J}'^T\boldsymbol{J}'\Delta\boldsymbol{x} &= -\boldsymbol{J}'^T\boldsymbol{e}'
\end{aligned}
$$
因此,只需要将信息矩阵的均方根左乘误差作为新的误差即可。所以观测边除了保存观测值以外还需要保存这个约束对应的信息矩阵的均方根。函数中 residual_eigen.applyOnTheLeft(sqrt_info_.template cast<T>()); 这一步就是将新矩阵的均方根左乘在误差上。观测边的类中除了要保存观测量以及信息矩阵,以及实现误差计算方式以外,还可以提供的一个 ceres::CostFunction* 的工厂函数,用于直接生成问题需要的残差函数指针,这里工厂函数返回一个 ceres::AutoDiffCostFunction<PriorPositionEdge, 3, 3> 类,模板中第一项为边的类型,第二个参数为残差维度,这里是位置残差因此维度为 3,第三个参数为关联的节点的参数维度。这里注意如果没有对优化变量参数进行特殊参数化,信息矩阵的参数顺序要和待优化的参数顺序的一致。
相对位姿的观测边
相对位姿的观测边定义如下,主要根据 Ceres Solver 的官方例子进行简单修改:
class RelativePoseEdge {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
RelativePoseEdge(const PoseSE3& measurement, const Eigen::Matrix<double, 6, 6>& sqrt_information)
: measurement_(measurement), sqrt_information_(sqrt_information) {}
template <typename T>
bool operator()(const T* const p_a_ptr,
const T* const q_a_ptr,
const T* const p_b_ptr,
const T* const q_b_ptr,
T* residuals_ptr) const {
Eigen::Map<const Eigen::Matrix<T, 3, 1>> p_a(p_a_ptr);
Eigen::Map<const Eigen::Quaternion<T>> q_a(q_a_ptr);
Eigen::Map<const Eigen::Matrix<T, 3, 1>> p_b(p_b_ptr);
Eigen::Map<const Eigen::Quaternion<T>> q_b(q_b_ptr);
// Compute the relative transformation between the two frames.
Eigen::Quaternion<T> q_a_inverse = q_a.conjugate();
Eigen::Quaternion<T> q_ab_estimated = q_a_inverse * q_b;
// Represent the displacement between the two frames in the A frame.
Eigen::Matrix<T, 3, 1> p_ab_estimated = q_a_inverse * (p_b - p_a);
// Compute the error between the two orientation estimates.
Eigen::Quaternion<T> delta_q = measurement_.quat.template cast<T>() * q_ab_estimated.conjugate();
// Compute the residuals.
// [ position ] [ delta_p ]
// [ orientation (3x1)] = [ 2 * delta_q(0:2) ]
Eigen::Map<Eigen::Matrix<T, 6, 1>> residuals(residuals_ptr);
residuals.template block<3, 1>(0, 0) = p_ab_estimated - measurement_.pos.template cast<T>();
residuals.template block<3, 1>(3, 0) = T(2.0) * delta_q.vec();
// Scale the residuals by the measurement uncertainty.
residuals.applyOnTheLeft(sqrt_information_.template cast<T>());
return true;
}
static ceres::CostFunction* Create(const PoseSE3& measurement,
const Eigen::Matrix<double, 6, 6>& sqrt_information) {
return new ceres::AutoDiffCostFunction<RelativePoseEdge, 6, 3, 4, 3, 4>(
new RelativePoseEdge(measurement, sqrt_information));
}
private:
// The measurement for the position of B relative to A in the A frame.
const PoseSE3 measurement_;
// The square root of the measurement information matrix.
const Eigen::Matrix<double, 6, 6> sqrt_information_;
};
大致思路是一致的,观测边中保存观测量(相对位姿)以及信息矩阵的均方根。然后定义误差计算函数以及工厂函数用于生成残差函数。在误差计算上,这里将每个位姿看成两个参数块,分别是平移(3维)以及旋转(四维),因此相对位姿观测总共约束 4 个参数块。这里我们也可以将位姿视为一个 7 维的参数块,但是由于本身位置是一个普通的三维向量,不用定义特殊的参数化方式,所以将其分开实现起来比较灵活。下面来看一下观测的误差的计算方式:给定两个位姿以及相对位姿观测 $\boldsymbol{q}_a, \boldsymbol{t}_a, \boldsymbol{q}_b, \boldsymbol{t}_b, \boldsymbol{q}_{ab}, \boldsymbol{t}_{ab}$,通过两个位姿能够计算出相对位姿:
$$
\begin{aligned}
\boldsymbol{T}'_{ab} &= \boldsymbol{T}_{wa}^{-1}\boldsymbol{T}_{wb}\\
&=
\begin{bmatrix}
\boldsymbol{R}_{wa}^{-1} & -\boldsymbol{R}^{-1}_{wa}\boldsymbol{t}_{wa}\\
\boldsymbol{0} & 1
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{R}_{wb} & \boldsymbol{t}_{wb}\\
\boldsymbol{0} & 1
\end{bmatrix}\\
&=
\begin{bmatrix}
\boldsymbol{R}_{wa}^{-1}\boldsymbol{R}_{wb} & \boldsymbol{R}_{wa}^{-1}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa})\\
\boldsymbol{0} & 1
\end{bmatrix}
\\
\Rightarrow \boldsymbol{q}'_{ab} &= \boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\\
\boldsymbol{t}'_{ab} &= \boldsymbol{R}^{-1}_{wa}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa})
\end{aligned}
$$
通过将计算出来的相对位姿和观测得到的相对位姿进行比较即可得到误差,位置误差很简单,两个三维向量相减即可;但是四元数本身只有三个自由度,因此是过参数化的。我们知道当其是小量时,四元数和旋转矢量的关系是:$\boldsymbol{q} = \begin{bmatrix}\frac{1}{2}\boldsymbol{\theta} & 1 \end{bmatrix}^T$,因此可以将误差转为李代数的形式,如下所示:
$$
\begin{aligned}
\Delta\boldsymbol{t} &= \boldsymbol{t}'_{ab} - \boldsymbol{t}_{ab} = \boldsymbol{R}^{-1}_{wa}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa}) - \boldsymbol{t}_{ab}\\
\Delta\boldsymbol{\theta} &= 2*(\boldsymbol{q}_{ab}'^{-1}\otimes \boldsymbol{q}_{ab})_{xyz} = 2(\boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
\boldsymbol{e}(\boldsymbol{T}_{wa}, \boldsymbol{T}_{wb}) &=
\begin{bmatrix}
\Delta\boldsymbol{t}\\
\Delta\boldsymbol{\theta}
\end{bmatrix}
\end{aligned}
$$
结合代码来看一下,由于四元数的逆为其共轭,因此我们用共轭运算获取第一个姿态的逆,并计算相对姿态变化:
Eigen::Quaternion<T> q_a_inverse = q_a.conjugate();
Eigen::Quaternion<T> q_ab_estimated = q_a_inverse * q_b;
相对平移很好计算,这里需要注意,四元数对向量进行旋转的方式是 $\boldsymbol{t}' = \boldsymbol{q}\otimes\boldsymbol{t}\otimes\boldsymbol{q}^{-1}$,但是 Eigen 库里面已经对四元数的 * 操作进行重载,所以可以直接计算:
Eigen::Matrix<T, 3, 1> p_ab_estimated = q_a_inverse * (p_b - p_a);
接下来和观测量比较,计算误差,四元数的 .vec() 操作为返回它的虚部作为三维向量:
// Compute the error between the two orientation estimates.
Eigen::Quaternion<T> delta_q = measurement_.quat.template cast<T>() * q_ab_estimated.conjugate();
// Compute the residuals.
// [ position ] [ delta_p ]
// [ orientation (3x1)] = [ 2 * delta_q(0:2) ]
Eigen::Map<Eigen::Matrix<T, 6, 1>> residuals(residuals_ptr);
residuals.template block<3, 1>(0, 0) = p_ab_estimated - measurement_.pos.template cast<T>();
residuals.template block<3, 1>(3, 0) = T(2.0) * delta_q.vec();
最后左乘上信息矩阵的均方根,这里信息矩阵共六行,按顺序其几何意义分别是x, y, z 轴的平移误差信息,x, y, z 轴的旋转误差信息(按左前上的坐标轴定义为 roll, pitch , yaw),和误差定义顺序一致:
residuals.applyOnTheLeft(sqrt_information_.template cast<T>());
观测误差的雅可比矩阵推导
注意事项
在优化时,给定一个迭代量 $\delta\boldsymbol{\psi} = \begin{bmatrix}\delta\boldsymbol{\theta} & \delta\boldsymbol{t}\end{bmatrix}$我们有两种旋转,一种是将位姿作为整体来进行优化,即:
$$
\begin{aligned}
\boldsymbol{T}&\leftarrow\exp{(\delta\boldsymbol{\psi}^\wedge)}\boldsymbol{T}\\
\begin{bmatrix}
\boldsymbol{R} & \boldsymbol{t} \\
\boldsymbol{0} & 1
\end{bmatrix}&\leftarrow
\begin{bmatrix}
\exp{(\boldsymbol{\delta\boldsymbol{\theta}^\wedge})} & \boldsymbol{J}\delta\boldsymbol{t}\\
\boldsymbol{0} & 1
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{R} & \boldsymbol{t} \\
\boldsymbol{0} & 1
\end{bmatrix}
\approx
\begin{bmatrix}
\exp{(\boldsymbol{\delta\boldsymbol{\theta}^\wedge})}\boldsymbol{R} & \exp{(\boldsymbol{\delta\boldsymbol{\theta}^\wedge})} \boldsymbol{t} + \delta\boldsymbol{t}\\
\boldsymbol{0} & 1
\end{bmatrix}\\
\boldsymbol{q}&\leftarrow\delta\boldsymbol{q} * \boldsymbol{q}\\
\boldsymbol{t}&\leftarrow\delta\boldsymbol{q} * \boldsymbol{t} + \delta\boldsymbol{t}
\end{aligned}
$$
另一种方法是将位姿分成独立的平移和旋转参数分别进行优化,即:
$$
\begin{aligned}
\boldsymbol{q} &\leftarrow \begin{bmatrix}
\cos{(\theta)} \\
\sin{(\theta)}\boldsymbol{n}
\end{bmatrix} \otimes \boldsymbol{q}\\
\boldsymbol{t} &\leftarrow \delta\boldsymbol{t} + \boldsymbol{t}
\end{aligned}
$$
这两种更新方法会影响后续雅可比的推导,如果是同步更新,那么在推导雅可比时需要同时加扰动,不能固定一个只对另一个进行求导。如果是独立更新,那么我们在求雅可比时可以视为两个独立变量,先固定一个分量对另一个分量求导,然后再反过来。
这里由于我们对旋转和平移是分开处理的,因此可以独立求导。
平移约束对位姿的雅可比推导
对单个位姿的位置(平移分量)的观测误差的雅可比推导很简单,只需要加平移分量上加扰动进行线性化即可:
$$
\begin{aligned}
\boldsymbol{e}(\boldsymbol{T}) &= t - \boldsymbol{t}'\\
&= (t + \delta t) - \boldsymbol{t}'\\
&= \boldsymbol{e}(\boldsymbol{T}_0) + \delta t\\
\Rightarrow \boldsymbol{J}^p &= \boldsymbol{I}\\
\boldsymbol{J}^q &= \boldsymbol{0}
\end{aligned}
$$
由于误差和旋转分量没有关系,因此对旋转部分的雅可比为零矩阵。
相对位姿约束对前后位姿的雅可比推导
对两个位姿的相对位姿误差的雅可比推导由于涉及到四元数,相对复杂一点。旋转部分涉及到四元数的预算,可以参考我之前对 vins-mono 中的雅可比推导 VIO 中残差雅可比的推导,误差函数如下所示:
$$
\begin{aligned}
\Delta\boldsymbol{t} &= \boldsymbol{t}'_{ab} - \boldsymbol{t}_{ab} = \boldsymbol{R}^{-1}_{wa}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa}) - \boldsymbol{t}_{ab}\\
\Delta\boldsymbol{\theta} &= 2*(\boldsymbol{q}_{ab}'^{-1}\otimes \boldsymbol{q}_{ab})_{xyz} = 2(\boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
\boldsymbol{e}(\boldsymbol{T}_{wa}, \boldsymbol{T}_{wb}) &=
\begin{bmatrix}
\Delta\boldsymbol{t}\\
\Delta\boldsymbol{\theta}
\end{bmatrix}
\end{aligned}
$$
我们需要通过添加微小扰动的方式(由于更新采用左乘,因此需要添加左扰动)来对误差方程进行线性化,从而推导对两个位姿的雅可比矩阵,如下所示:
$$
\begin{aligned}
\boldsymbol{e}(\boldsymbol{T}_{wa}, \boldsymbol{T}_{wb}) &=
\begin{bmatrix}
\boldsymbol{R}^{-1}_{wa}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa}) - \boldsymbol{t}_{ab}\\
2(\boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}
\end{bmatrix}\\
&= \boldsymbol{e}(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0) + \boldsymbol{J}^a_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}\boldsymbol{\phi}_a + \boldsymbol{J}^b_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}\boldsymbol{\phi}_b\\
\boldsymbol{J}^a_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} &=
\begin{bmatrix}
\boldsymbol{J}^{\boldsymbol{R}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} & \boldsymbol{J}^{\boldsymbol{t}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}
\end{bmatrix} \in \mathbb{R}^{6\times6}\\
\boldsymbol{J}^b_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} &=
\begin{bmatrix}
\boldsymbol{J}^{\boldsymbol{R}b}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} & \boldsymbol{J}^{\boldsymbol{t}b}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}
\end{bmatrix}\in \mathbb{R}^{6\times6}
\end{aligned}
$$
如上所示,可以分为四个部分解决分别为:
- 残差对
$\boldsymbol{R}_{wa}$的雅可比:$\boldsymbol{J}^{\boldsymbol{R}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}$ - 残差对
$\boldsymbol{t}_{wa}$的雅可比:$\boldsymbol{J}^{\boldsymbol{t}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}$ - 残差对
$\boldsymbol{R}_{wb}$的雅可比:$\boldsymbol{J}^{\boldsymbol{R}b}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}$ - 残差对
$\boldsymbol{t}_{wb}$的雅可比:$\boldsymbol{J}^{\boldsymbol{t}b}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)}$
其中,每一部分可以将残差分为旋转误差和平移误差两部分进行推导
下面分别来看,首先看比较简单的平移部分的雅可比矩阵:
残差对 $\boldsymbol{t}_{wa}$ 的雅可比,如下所示:
$$
\begin{aligned}
\boldsymbol{e}_{t} = \Delta\boldsymbol{t} &= \boldsymbol{R}^{-1}_{wa}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa}) - \boldsymbol{t}_{ab}\\
&=(\boldsymbol{R}^0_{wa})^{-1}(\boldsymbol{t}^0_{wb} - (\boldsymbol{t}^0_{wa} + \delta\boldsymbol{t})) - \boldsymbol{t}_{ab}\\
&= \Delta\boldsymbol{t}_0 - (\boldsymbol{R}^0_{wa})^{-1}\delta\boldsymbol{t}\\
\boldsymbol{e}_{R} = \Delta\boldsymbol{\boldsymbol{\theta}} &= 2(\boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
&= \Delta\boldsymbol{\boldsymbol{\theta}}_0 + \boldsymbol{0}\delta\boldsymbol{t}\\
\Rightarrow \boldsymbol{J}^{\boldsymbol{t}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} &=
\begin{bmatrix}
-(\boldsymbol{R}^0_{wa})^{-1}\\
\boldsymbol{0}
\end{bmatrix} \in \mathbb{R}^{6 \times 3}
\end{aligned}
$$
残差对 $\boldsymbol{t}_{wb}$ 的雅可比,如下所示:
$$
\begin{aligned}
\boldsymbol{e}_{t} = \Delta\boldsymbol{t} &= \boldsymbol{R}^{-1}_{wa}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa}) - \boldsymbol{t}_{ab}\\
&=(\boldsymbol{R}^0_{wa})^{-1}((\boldsymbol{t}^0_{wb}+ \delta\boldsymbol{t}) - \boldsymbol{t}^0_{wa}) - \boldsymbol{t}_{ab}\\
&= \Delta\boldsymbol{t}_0 + (\boldsymbol{R}^0_{wa})^{-1}\delta\boldsymbol{t}\\
\boldsymbol{e}_{R} = \Delta\boldsymbol{\boldsymbol{\theta}} &= 2(\boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
&= \Delta\boldsymbol{\boldsymbol{\theta}}_0 + \boldsymbol{0}\delta\boldsymbol{t}\\
\Rightarrow \boldsymbol{J}^{\boldsymbol{t}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} &=
\begin{bmatrix}
(\boldsymbol{R}^0_{wa})^{-1}\\
\boldsymbol{0}
\end{bmatrix} \in \mathbb{R}^{6 \times 3}
\end{aligned}
$$
接下来推导残差对两位姿中旋转分量的雅可比矩阵。
残差对 $\boldsymbol{q}_{wa}$ 的雅可比,如下所示:
先对残差中的平移分量进行线性化:
$$
\begin{aligned}
\boldsymbol{e}_{t} = \Delta\boldsymbol{t} &= \boldsymbol{R}^{-1}_{wa}(\boldsymbol{t}_{wb} - \boldsymbol{t}_{wa}) - \boldsymbol{t}_{ab}\\
&=(\exp{(\boldsymbol{\phi}^\wedge)}\boldsymbol{R}^0_{wa})^{-1}(\boldsymbol{t}^0_{wb} - \boldsymbol{t}^0_{wa}) - \boldsymbol{t}_{ab}\\
&=(\boldsymbol{R}^0_{wa})^{-1}\exp{(-\boldsymbol{\phi}^\wedge)}(\boldsymbol{t}^0_{wb} - \boldsymbol{t}^0_{wa}) - \boldsymbol{t}_{ab}\\
&\approx(\boldsymbol{R}^0_{wa})^{-1}(\boldsymbol{I} -\boldsymbol{\phi}^\wedge)(\boldsymbol{t}^0_{wb} - \boldsymbol{t}^0_{wa}) - \boldsymbol{t}_{ab}\\
&= \Delta\boldsymbol{t}_0 - (\boldsymbol{R}^0_{wa})^{-1}\boldsymbol{\phi}^\wedge(\boldsymbol{t}^0_{wb}- \boldsymbol{t}^0_{wa})\\
&= \Delta\boldsymbol{t}_0 + (\boldsymbol{R}^0_{wa})^{-1}(\boldsymbol{t}^0_{wb}- \boldsymbol{t}^0_{wa})^\wedge\boldsymbol{\phi}
\end{aligned}
$$
接下来对残差中的旋转分量进行线性化:
$$
\begin{aligned}
\boldsymbol{e}_{R} = \Delta\boldsymbol{\boldsymbol{\theta}} &= 2(\boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
&= 2((
\begin{bmatrix}
1 \\ \frac{1}{2}\delta\boldsymbol{\theta}
\end{bmatrix}\otimes\boldsymbol{q}_{wa})^{-1} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
&= 2(\boldsymbol{q}_{wa}^* \otimes\begin{bmatrix}
1 \\ \frac{1}{2}\delta\boldsymbol{\theta}
\end{bmatrix}^*\otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
&= (2[\boldsymbol{q}_{wa}^*]_L[\boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab}]_R
\begin{bmatrix}
1 \\ -\frac{1}{2}\delta\boldsymbol{\theta}
\end{bmatrix})_{xyz}\\
&= (2[\boldsymbol{q}_{wa}^*]_L[\boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab}]_R
(\begin{bmatrix}
1 \\ \boldsymbol{0}
\end{bmatrix} +
\begin{bmatrix}
0 \\ -\frac{1}{2}\delta\boldsymbol{\theta}
\end{bmatrix}))_{xyz}\\
&= \Delta\boldsymbol{\boldsymbol{\theta}}_0 - ([\boldsymbol{q}_{wa}^*]_L[\boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab}]_R)_{3\times3}(\delta\boldsymbol{\theta})
\end{aligned}
$$
将两部分结合起来,有:
$$
\boldsymbol{J}^{\boldsymbol{R}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} =
\begin{bmatrix}
(\boldsymbol{R}^0_{wa})^{-1}(\boldsymbol{t}^0_{wb}- \boldsymbol{t}^0_{wa})^\wedge\\
-([\boldsymbol{q}_{wa}^*]_L[\boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab}]_R)_{3\times3}
\end{bmatrix} \in \mathbb{R}^{6\times3}
$$
残差对 $\boldsymbol{q}_{wb}$ 的雅可比,如下所示:
先对残差中的平移分量与 $\boldsymbol{q}_{wb}$ 无关, 对应雅可比矩阵为零矩阵 $\boldsymbol{0}_{3\times3}$:
接下来对残差中的旋转分量进行线性化:
$$
\begin{aligned}
\boldsymbol{e}_{R} = \Delta\boldsymbol{\boldsymbol{\theta}} &= 2(\boldsymbol{q}^{-1}_{wa} \otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
&= 2(\boldsymbol{q}_{wa}^{-1} \otimes\begin{bmatrix}
1 \\ \frac{1}{2}\delta\boldsymbol{\theta}
\end{bmatrix}\otimes \boldsymbol{q}_{wb}\otimes \boldsymbol{q}_{ab})_{xyz}\\
&= (2[\boldsymbol{q}_{wa}^*]_L[ \boldsymbol{q}_{wb}\otimes\boldsymbol{q}_{ab}]_R
\begin{bmatrix}
1 \\ \frac{1}{2}\delta\boldsymbol{\theta}
\end{bmatrix})_{xyz}\\
&= (2[\boldsymbol{q}_{wa}^*]_L[ \boldsymbol{q}_{wb}\otimes\boldsymbol{q}_{ab}]_R
(\begin{bmatrix}
1 \\ \boldsymbol{0}
\end{bmatrix} +
\begin{bmatrix}
0 \\ \frac{1}{2}\delta\boldsymbol{\theta}
\end{bmatrix}))_{xyz}\\
&= \Delta\boldsymbol{\boldsymbol{\theta}}_0 + ([\boldsymbol{q}_{wa}^*]_L[ \boldsymbol{q}_{wb}\otimes\boldsymbol{q}_{ab}]_R)_{3\times3}(\delta\boldsymbol{\theta})
\end{aligned}
$$
将两部分结合起来,有:
$$
\boldsymbol{J}^{\boldsymbol{R}a}_{(\boldsymbol{T}_{wa}^0, \boldsymbol{T}_{wb}^0)} =
\begin{bmatrix}
\boldsymbol{0}_{3\times3}\\
([\boldsymbol{q}_{wa}^*]_L[ \boldsymbol{q}_{wb}\otimes\boldsymbol{q}_{ab}]_R)_{3\times3}
\end{bmatrix} \in \mathbb{R}^{6\times3}
$$
解析求导的具体实现
TODO
Ceres 添加点和边以及进行优化的过程
有了点和边,使用 Ceres 进行图优化的准备就做好了,优化的过程分为以下几步,源代码见 ceres_graph_optimizer.hpp:
首先,初始化问题类,优化选项以及优化总结,以及设置对四元数的参数化
ceres::Problem problem_;
ceres::Solver::Options options_;
ceres::Solver::Summary summary_;
ceres::LocalParameterization *quaternion_local_parameterization_ = new ceres::EigenQuaternionParameterization;
接下来,对每一个节点加入参数块(节点),这里注意传入进去的是地址,因此参数块本身是在外部维护的。对需要固定的节点(比如没有先验信息约束下的第一个节点),可以对其设置为固定:
void CeresGraphOptimizer::AddSe3Node(const Eigen::Isometry3d &pose, bool need_fix) {
vertices_.push_back(PoseSE3());
PoseSE3 &pose_se3 = vertices_.back();
pose_se3.pos = pose.translation();
pose_se3.quat = pose.rotation();
// 传入进去的是地址!
problem_.AddParameterBlock(pose_se3.pos.data(), 3);
problem_.AddParameterBlock(pose_se3.quat.coeffs().data(), 4);
// 对四元数对应的参数块进行局部参数化设置
problem_.SetParameterization(pose_se3.quat.coeffs().data(), quaternion_local_parameterization_);
// 对需要固定的参数块设置为常值
if (need_fix) {
problem_.SetParameterBlockConstant(vertices_.back().pos.data());
problem_.SetParameterBlockConstant(vertices_.back().quat.coeffs().data());
}
}
加入残差块(边),按需设置鲁棒核函数
ceres::LossFunction *loss_function_ = nullptr;
// 按需设置鲁棒核函数
// need_robust_kernel_ = true;
// loss_function_ = new ceres::HuberLoss(1.0);
void CeresGraphOptimizer::AddSe3Edge(int vertex_index1,
int vertex_index2,
const Eigen::Isometry3d &relative_pose,
const Eigen::Vector3d &translation_noise,
const Eigen::Vector3d &rotation_noise) {
// 获取对应的参数块地址(必须是引用)
PoseSE3 &v1 = vertices_[vertex_index1];
PoseSE3 &v2 = vertices_[vertex_index2];
PoseSE3 measurement;
measurement.pos = relative_pose.translation();
measurement.quat = relative_pose.rotation();
// 设置信息矩阵
Eigen::Matrix<double, 6, 1> noise;
noise << translation_noise, rotation_noise;
Eigen::Matrix<double, 6, 6> sqrt_info = CalculateSqrtDiagMatrix(noise);
// 生成残差函数
ceres::CostFunction *cost_function = RelativePoseEdge::Create(measurement, sqrt_info);
// 将残差函数加入问题中
problem_.AddResidualBlock(
cost_function, loss_function_, v1.pos.data(), v1.quat.coeffs().data(), v2.pos.data(), v2.quat.coeffs().data());
}
设置迭代策略和线性方程组求解方式并进行优化
options.linear_solver_type = ceres::SPARSE_NORMAL_CHOLESKY; // 可选其他方法如 QR
options_.trust_region_strategy_type = ceres::TrustRegionStrategyType::LEVENBERG_MARQUARDT;
ceres::Solve(options_, &problem_, &summary_);