因子图引入
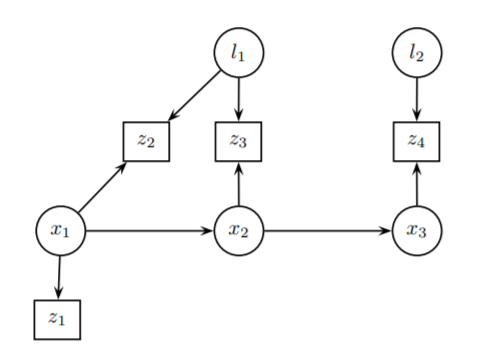
首先我们对一个 SLAM 问题使用贝叶斯网络进行建模,如下图所示,一个移动机器人(载体)在运动过程中对一系列路标进行观测:
其中,$x$ 是待估计的载体状态量, $l$ 是路标,$z$ 是载体对路标的观测。因此,我们可以得到下式:
$$
P(X, Z) = P(x_0)\prod_{i=1}P(x_i|x_{i-1}, u)\prod_{k=1}P(z_k|x_{i_k},l_{j_k})
$$
其中,对 $x_i$ 和 $z_i$ 我们可以分别用运动模型和观测对其进行建模:
$$
\begin{aligned}
x_i &= f_i(x_{i-1}, u_i) + w_i\\
z_k &= h_k(x_{i_k}, l_{j_k}) + v_k
\end{aligned}
$$
上式中,假设在运动和观测模型中存在高斯白噪声 $w, v$,因此这里我们可以使用随机变量对状态量和观测量进行描述,并且其符合高斯分布,则有:
$$
\begin{aligned}
P(x_i | x_{i-1}, u_i) &\propto \exp{-\frac{1}{2}||f_i(x_{i-1}, u_i) - x_i||_{\Delta i}^2}\\
P(z_i | x_{i_k}, l_{j_k}) &\propto \exp{-\frac{1}{2}||h_k(x_{i_k}, l_{j_k}) - z_k||_{\Delta k}^2}
\end{aligned}
$$
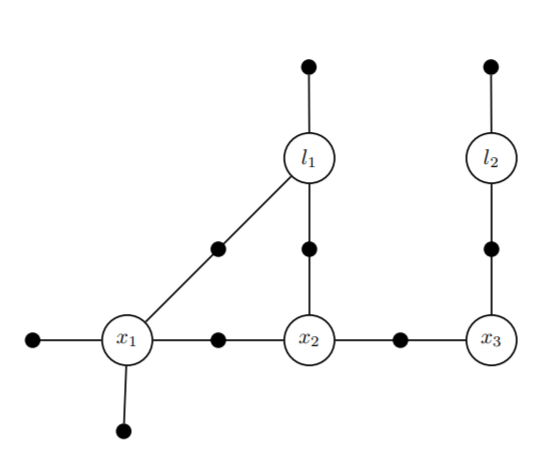
在上图中,我们把观测单独作为一类节点,而两状态之间由于运动模型产生的变化没有体现,这样并不是很直观。并且由 $P(X, Z)$ 的计算式中,我们可以发现实际上 $P(X, Z)$ 是由一系列运动模型和观测模型的条件概率相乘得到的。因此很质感的我们想把连乘式中所有的因子从状态量中分离出来,作为单独的一类分析。这就是因子图的起因,在因子图中我们将不同模块分为两部分:因子(factor)和变量(variables)。每一个因子对应一个上式贝叶斯网络中的概率,并且每一个因子只和与其有关系的节点相连,因此上式贝叶斯网络转化为因子图,如下所示:
使用$\theta$ 作为变量,包括 $x, l$ $\phi(\theta)$ 作为因子的表示方式,则对全局概率有:
$$
\begin{aligned}
P(\Theta) &\propto \prod_i\phi_i(\theta_i)\prod_{\{i, j\}, i <j}\phi_{ij}(\theta_i, \theta_j)\\
\phi_0(x_o) &\propto P(x_0)\\
\phi_j(l_j) &\propto P(l_j)\\
\phi_{(i-1),i}(x_{i-1}, x_i) &\propto P(x_i|x_{i-1}, u_i)\\
\phi_{i_kj_k}(x_{i_k}, l_{j_k}) &\propto P(z_k|x_{i_k}, l_{j_k})
\end{aligned}
$$
接下来我们要估计最大后验概率出现的位置,即找到一个状态量使得各个因子相乘的概率值最大,即求解:
$$
\begin{aligned}
\Theta^* &= \arg\max_{\Theta}f(\Theta)\\
f(\Theta) &= \prod_if_i(\theta)\\
f_i(\theta) &\propto\exp{\left(-\frac{1}{2}||h_i(\Theta_i) - z_i||_{\Sigma i}^2\right)}
\end{aligned}
$$
对该式进行化简可以得到:
$$
\begin{aligned}
\Theta^* &= \arg\max_{\Theta}f(\Theta)\\
&= \arg\max_{\Theta}\left(\prod_if_i(\theta)\right)\\
&= \arg\max_{\Theta}\left(\prod_i\exp{\left(-\frac{1}{2}||h_i(\Theta_i) - z_i||_{\Sigma i}^2\right)}\right)\\
&= \arg\max_{\Theta}\left(\sum_i\left(-\frac{1}{2}||h_i(\Theta_i) - z_i||_{\Sigma i}^2\right)\right)\\
&= \arg\min_{\Theta}\left(\frac{1}{2}\sum_i||h_i(\Theta_i) - z_i||_{\Sigma i}^2\right)\\
\end{aligned}
$$
因此,我们将这个最大后验概率问题转化成了一个最小二乘问题。可以采用最小二乘问题的问题进行求解。
iSAM
未完待续。