简介
前两篇博客分别整理了 IMU 的测量原理和误差形成原因,接下来主要关注如何对 IMU 进行标定和校正。
确定误差标定
在之前的博客中,我们总结了 IMU 的误差模型如下所示。这一部分中是对零偏、尺度因子和轴偏差矩阵进行标定,对于噪声(包括测量值中的白噪声和零偏不稳定性)我们无法通过校正来消除,只能通过计算其不确定度来作为我们参考的指标。
$$
\begin{aligned}
\boldsymbol{a}^O &= \boldsymbol{T}^a\boldsymbol{K}^a(\boldsymbol{a}^S + \boldsymbol{b}^a + \boldsymbol{n}^a) \\
\boldsymbol{\omega}^O &= \boldsymbol{T}^\omega\boldsymbol{K}^\omega(\boldsymbol{\omega} + \boldsymbol{b}^a + \boldsymbol{n}^a)
\end{aligned}
$$
为了简化计算,我们可以将尺度因子和轴偏差矩阵融合进零偏中先进行计算,标定好尺度因子和轴偏差之后再用起算起零偏即可,即令 $\boldsymbol{B} = \boldsymbol{T}\boldsymbol{K}\boldsymbol{b}$:
$$
\begin{aligned}
\boldsymbol{a}^O &= \boldsymbol{T}^a\boldsymbol{K}^a\boldsymbol{a}^S + \boldsymbol{B}^a \\
\boldsymbol{\omega}^O &= \boldsymbol{T}^\omega\boldsymbol{K}^\omega\boldsymbol{\omega} + \boldsymbol{B}^g
\end{aligned}
$$
常规解方程方法
这一种方法比较直观,简单的说我们需要解出以下方程组的系数,以加速度计为例:
$$
\begin{aligned}
\begin{bmatrix}
a_x^O\\
a_y^O\\
a_z^O
\end{bmatrix} =
\begin{bmatrix}
1 & -\beta_{yz}^a & \beta_{zy}^a \\
\beta_{xz}^a & 1 & -\beta_{zx}^a \\
-\beta_{xy}^a & \beta_{yx}^a & 1
\end{bmatrix}
\begin{bmatrix}
s_x^a & 0 & 0 \\
0 & s_y^a & 0 \\
0 & 0 & s_z^a
\end{bmatrix}
\begin{bmatrix}
a_x^S\\
a_y^S\\
a_z^S
\end{bmatrix} +
\begin{bmatrix}
B_x\\
B_y\\
B_z
\end{bmatrix}
\end{aligned}
$$
如上所示,我们需要求解上述三个联立方程中的 12 个独立参数。因此理论上最少我们只需要获取四组加速度计的数据(互相独立的情况下),联立方程即可。实际中一般有两种思路:
解析法(加速度计)
这个方法中我们需要利用准确的真值和理论值来进行求解,并且需要将上述方程改变一下将真值作为自变量简化计算,如下所示:
$$
\begin{aligned}
\boldsymbol{a}^S &= (\boldsymbol{T}^a\boldsymbol{K}^a)^{-1}\boldsymbol{a}^O - \boldsymbol{b}^a \\
&= \boldsymbol{T}'\boldsymbol{a}^O + \boldsymbol{b}'^{a}\\
&= \begin{bmatrix}
s_x'^a & \beta'^a_{yz} & \beta'^a_{zy} \\
\beta'^a_{xz} & s_y'^a & \beta'^a_{zx} \\
\beta'^a_{xy} & \beta'^a_{yx} & s_z'^a
\end{bmatrix}\boldsymbol{a}^O+
\begin{bmatrix}
b'^a_x\\
b'^a_y\\
b'^a_z
\end{bmatrix}
\end{aligned}
$$
这里注意,实际上有些工具或者论文可能是以这种表示方法作为误差模型,即将真实值作为方程自变量,测量值作为因变量。实际上两者应该互相等效,只需要前后保持一致即可,这里在总结不同方法时为了方便计算可能会转换成不同表示方法。首先将 IMU 水平向上放置,此时理论加速度为:$(0, 0, g)$,代入上述方程有:
$$
\begin{aligned}
a^S_x &= \beta'^a_{zy}g+b'^a_x \\
a^S_y &= \beta'^a_{zx}g+b'^a_x \\
a^S_z &= s_z'^ag+b'^a_x
\end{aligned}
$$
同理,将 IMU 倒立放置,此时理论加速度为:$(0, 0, -g)$,代入为:
$$
\begin{aligned}
a'^S_x &= -\beta'^a_{zy}g+b'^a_x \\
a'^S_y &= -\beta'^a_{zx}g+b'^a_x \\
a'^S_z &= -s_z'^ag+b'^a_x
\end{aligned}
$$
两组方程式联立即可求出 6 个独立参数,对于其他参数,可以参考这个做法将对应轴方向或者向下放置求解即可。这个方法要求加速度计必须得放平,对平台有一定的要求。
线性最小二乘(加速度计)
线性最小二乘的方法则不依赖于某个特定角度,将误差模型整理成以下形式:
$$
\begin{aligned}
&\begin{aligned}
a_x^O &= s_x^aa_x^S -\beta_{yz}^aa_y^S + \beta^a_{zy}a_z^S + b_x^a \\
a_y^O &= \beta_{xz}^aa_x^S -s_y^aa_y^S + -\beta_{zx}^aa_z^S + b_y^a \\
a_z^O &= -\beta_{xy}^aa_x^S -\beta_{yx}^aa_y^S + s_z^aa_z^S + b_z^a
\end{aligned}\\
&\Downarrow
\\
\begin{bmatrix}
a_x^O\\
a_y^O\\
a_z^O
\end{bmatrix} &=
\begin{bmatrix}
a_x^S & a_y^S & a_z^S & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & a_x^S & a_y^S & a_z^S & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & a_x^S & a_y^S & a_z^S & 1
\end{bmatrix}
\begin{bmatrix}
s_x^a\\
-\beta_{yz}^a\\
\beta^a_{zy}\\
b_x^a\\
\beta_{xz}^a\\
-s_y^a\\
-\beta_{zx}^a\\
b_y^a\\
-\beta_{xy}^a\\
-\beta_{yx}^a\\
s_z^a\\
b_z^a
\end{bmatrix}\\
&\Downarrow\\
\boldsymbol{b} &= \boldsymbol{A}\boldsymbol{x}
\end{aligned}
$$
通过这种方法我们将问题转换成一个典型的线性最小二乘问题:$\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}$,其最优解为:$\tilde{\boldsymbol{x}} = (\boldsymbol{A}^T\boldsymbol{A})^{-1}\boldsymbol{A}^T\boldsymbol{b}$
因此,将 IMU 用不同朝向获取一系列数据取得上述 $\boldsymbol{A}$ 和 $\boldsymbol{b}$ 求解即可,另外上述构建的方程只是其中最简单的一种,将参数排列顺序改变可以获得不同系数矩阵。
解析法(陀螺仪)
对于陀螺仪标定,大致思路和加速度计一致,但有以下两点区别:
- 不同于加速度计,陀螺仪没办法使用重力加速度作为真值,因此只能使用高精度转台来提供所需要的真值,而由于转台的角速度精度通常不如角度精度高,因此通常对角度进行积分得到角度作为真值
- 陀螺的角速度除了要考虑转台提供的角速度,还需要考虑地球自转的影响,通常的做法时通过构建特定的方程将地球转速抵消
同样为了化简计算,采用如下误差模型,这里假设地球转速对陀螺仪真值的影响为 $\boldsymbol{\omega}_e^i = (\omega_{ex}^i, \omega_{ey}^i, \omega_{ez})$:
$$
\begin{aligned}
\boldsymbol{\omega}^S &= (\boldsymbol{T}^g\boldsymbol{K}^g)^{-1}(\boldsymbol{\omega}^O + \boldsymbol{\omega}_e^i) - \boldsymbol{b}^g \\
&= \boldsymbol{T}'(\boldsymbol{\omega}^O + \boldsymbol{\omega}_e^i) + \boldsymbol{b}'^{g}\\
&= \begin{bmatrix}
s_x'^g & \beta'^g_{yz} & \beta'^g_{zy} \\
\beta'^g_{xz} & s_y'^a & \beta'^g_{zx} \\
\beta'^g_{xy} & \beta'^g_{yx} & s_z'^g
\end{bmatrix}(\boldsymbol{\omega}^O + \boldsymbol{\omega}_e^i)+
\begin{bmatrix}
b'^g_x\\
b'^g_y\\
b'^g_z
\end{bmatrix}
\end{aligned}
$$
先将陀螺仪沿 $z$ 轴正方向以角速度 $\omega$ 旋转,有:
$$
\begin{aligned}
\omega_x^S = \beta'^g_{zy}\omega + \begin{bmatrix}
s_x'^g & \beta'^g_{yz} & \beta'^g_{zy}
\end{bmatrix}\boldsymbol{\omega}_e^i + b'^g_x\\
\omega_x^S = \beta'^g_{zx}\omega + \begin{bmatrix}
\beta'^g_{xz} & s_y'^a & \beta'^g_{zx}
\end{bmatrix}\boldsymbol{\omega}_e^i + b'^g_y\\
\omega_x^S = s_z'^g\omega + \begin{bmatrix}
\beta'^g_{xy} & \beta'^g_{yx} & s_z'^g
\end{bmatrix}\boldsymbol{\omega}_e^i + b'^g_z
\end{aligned}
$$
对角速度积分,有:
$$
\begin{aligned}
\theta_x^S = \beta'^g_{zy}\theta + \begin{bmatrix}
s_x'^g & \beta'^g_{yz} & \beta'^g_{zy}
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{bx}\\
\theta_x^S = \beta'^g_{zx}\theta + \begin{bmatrix}
\beta'^g_{xz} & s_y'^a & \beta'^g_{zx}
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{by}\\
\theta_x^S = s_z'^g\theta + \begin{bmatrix}
\beta'^g_{xy} & \beta'^g_{yx} & s_z'^g
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{bz}
\end{aligned}
$$
同样思路,以角速度 $-\omega$ 旋转(相反方向)并积分,有:
$$
\begin{aligned}
\theta_x'^S = -\beta'^g_{zy}\theta + \begin{bmatrix}
s_x'^g & \beta'^g_{yz} & \beta'^g_{zy}
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{bx}\\
\theta_y'^S = -\beta'^g_{zx}\theta + \begin{bmatrix}
\beta'^g_{xz} & s_y'^a & \beta'^g_{zx}
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{by}\\
\theta_z'^S = -s_z'^g\theta + \begin{bmatrix}
\beta'^g_{xy} & \beta'^g_{yx} & s_z'^g
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{bz}
\end{aligned}
$$
两组方程相减,即可求得部分尺度因子和轴偏差参数,对于其他尺度因子和轴偏差参数,只需要将陀螺仪沿其他两轴用同样方式得到即可。注意这里不能像加速度计一样通过相加来获取零偏,有两点原因:地球转速未知、旋转时间过短零产生的角度太小,如果直接计算误差会很大。这里我们通过另一种方法求解:
假设地球沿自转轴自转角速度为 $\omega_e$,将其投影至东北天坐标系(正切与地球地球表面)的角速度为:
$$
\boldsymbol{\omega}^n =
\begin{bmatrix}
\omega^n_x \\
\omega^n_y \\
\omega^n_z \\
\end{bmatrix} =
\begin{bmatrix}
0 \\
\omega_e\cos{\phi} \\
\omega_e\sin{\phi}
\end{bmatrix}
$$
其中 $\phi$ 为 ENU 系原点所在的纬度。由 ENU 系至 IMU 系还需要一次旋转,这个旋转矩阵是未知的,设为 $\boldsymbol{R}$,则当陀螺仪处以某一位置,上述地球转速对陀螺仪形成的额外角速度为:
$$
\boldsymbol{\omega}^i_e = \boldsymbol{R}\begin{bmatrix}
\omega^n_x \\
\omega^n_y \\
\omega^n_z \\
\end{bmatrix}
$$
此时若我们将 陀螺仪沿其 $z$ 轴旋转 180 度,这个角速度为:
$$
\begin{aligned}
\boldsymbol{\omega}'^i_e &= \boldsymbol{R}_\pi\boldsymbol{R}\begin{bmatrix}
\omega^n_x \\
\omega^n_y \\
\omega^n_z \\
\end{bmatrix}\\
&= \begin{bmatrix}
\cos{\pi} & \sin{\pi} & 0\\
-\sin{\pi} & \cos{\pi} & 0\\
0 & 0 & 1
\end{bmatrix}\boldsymbol{R}\begin{bmatrix}
\omega^n_x \\
\omega^n_y \\
\omega^n_z \\
\end{bmatrix} \\
&= \begin{bmatrix}
-1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{bmatrix}\boldsymbol{R}\begin{bmatrix}
\omega^n_x \\
\omega^n_y \\
\omega^n_z \\
\end{bmatrix}\\
&= \boldsymbol{R}\begin{bmatrix}
-\omega^n_x \\
-\omega^n_y \\
\omega^n_z \\
\end{bmatrix}
\end{aligned}
$$
可以发现此时我们将 $x, y$ 轴上的地球角速度转变成其相反数,沿着这个思路,我们先将陀螺仪在某一位置停留一段时间,对其测量角速度(只包含零偏和地球自转角速度)进行积分,有:
$$
\begin{aligned}
\theta_x'^S = \begin{bmatrix}
s_x'^g & \beta'^g_{yz} & \beta'^g_{zy}
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{bx}\\
\theta_y'^S = \begin{bmatrix}
\beta'^g_{xz} & s_y'^a & \beta'^g_{zx}
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{by}\\
\theta_z'^S = \begin{bmatrix}
\beta'^g_{xy} & \beta'^g_{yx} & s_z'^g
\end{bmatrix}\boldsymbol{\theta}_e^i + \theta'^g_{bz}
\end{aligned}
$$
这里由于 $\beta\theta$ 是一个二阶小量所以可以省略,上式化简为:
$$
\begin{aligned}
\theta_x^S &= s_x'^g\theta_{ex}^i + \theta'^g_{bx}\\
\theta_y^S &= s_y'^g\theta_{ey}^i + \theta'^g_{by}\\
\theta_z^S &= s_z'^g\theta_{ez}^i + \theta'^g_{bz}
\end{aligned}
$$
将陀螺仪转过 180 度再停留一段时间,对测量角速度积分得:
$$
\begin{aligned}
\theta_x'^S &= -s_x'^g\theta_{ex}^i + \theta'^g_{bx}\\
\theta_y'^S &= -s_y'^g\theta_{ey}^i + \theta'^g_{by}\\
\theta_z'^S &= s_z'^g\theta_{ez}^i + \theta'^g_{bz}
\end{aligned}
$$
两组方程相加即可获得 $x, y$ 轴的零偏,接下来以其他两轴作为转轴旋转以同样方式即可得到 $z$ 轴的零偏。自此我们标定了陀螺仪的零偏,标度因子和轴偏差参数。
线性最小二乘法(陀螺仪)
线性最小二乘法跟加速度计的类似,将误差模型转化为 $\boldsymbol{Ax = b}$ 的形式再获取多组数据求解即可,地球对转速的影响同样可以作为待估计参数进行标定。
优化方法
除了用常规的解方程的思想去标定各个参数以外,我们还可以用优化的思路求解。
优化方法标定加速度计内参
前面我们假设加速度计的三个轴都有一定的轴偏差,这里我们使加速度计的 $x$ 轴和理想正交系的 $x$ 轴重合,并使加速度计的 $y$ 轴在理想正交系的 $x, y$ 轴形成的平面上,这个条件是可以通过旋转理想正交系满足的。此时轴偏差参数 $\beta_{xz}, \beta_{xy}, \beta_{yx}$ 变成 0,轴偏差矩阵为:
$$
\boldsymbol{T}^a=\begin{bmatrix}
1 & -\beta_{yz}^a & \beta_{zy}^a \\
0 & 1 & -\beta_{zx}^a \\
0 & 0 & 1
\end{bmatrix}
$$
因此,加速度计中需要标定的参数为:
$$
\boldsymbol{\theta}^a = \begin{bmatrix}
\beta_{yz}^a & \beta_{zy}^a & \beta_{zx}^a & s_x^a & s_y^a & s_z^a & b_x^a & b_y^a & b_z^a
\end{bmatrix}
$$
我们知道当 IMU 静止的时候,它输出的理论值的大小是当地的重力加速度大小,因此可以以这个作为优化条件,在不同角度下将 IMU 静置一段时间,采集 M 组数据,将测量值的大小和理论值的大小作为残差进行 LM 优化,即:
$$
\begin{aligned}
\boldsymbol{L}(\boldsymbol{\theta}^a) &= \sum_{k = 1}^M(||\boldsymbol{g}||^2 - ||h(\boldsymbol{a}_k^S, \boldsymbol{\theta}^a)||^2)^2 \\
h(\boldsymbol{a}_k^S, \boldsymbol{\theta}^a) &= \boldsymbol{T}^a\boldsymbol{K}^a(\boldsymbol{a}^S - \boldsymbol{b}^a)
\end{aligned}
$$
优化过程中需要计算残差的雅克比矩阵,这里的残差为:
$$
\begin{aligned}
\boldsymbol{e}^a &= ||\boldsymbol{g}||^2 - ||h(\boldsymbol{a}_k^S, \boldsymbol{\theta}^a)||^2 \\
&= ||\boldsymbol{g}||^2 - h(\boldsymbol{a}_k^S, \boldsymbol{\theta}^a)^Th(\boldsymbol{a}_k^S, \boldsymbol{\theta}^a)\\
&= ||\boldsymbol{g}||^2 - (\boldsymbol{T}^a\boldsymbol{K}^a(\boldsymbol{a}^S - \boldsymbol{b}^a))^T(\boldsymbol{T}^a\boldsymbol{K}^a(\boldsymbol{a}^S - \boldsymbol{b}^a))
\end{aligned}
$$
根据链式求导法则:
$$
\begin{aligned}
\frac{\partial\boldsymbol{e}^a}{\partial\boldsymbol{\theta}^a} &= \frac{\partial\boldsymbol{e}^a}{\partial h}\frac{\partial h}{\partial\boldsymbol{\theta}^a}\\
&= \frac{h^Th}{\partial h}\frac{\partial h}{\partial\boldsymbol{\theta}^a}\\
&= 2h^T\frac{\partial h}{\partial\boldsymbol{\theta}^a}
\end{aligned}
$$
问题转化为求 $h(\boldsymbol{a}_k^S, \boldsymbol{\theta}^a)$ 对内参的偏导,这里我没有想到比较好的化简思路,只能直接将向量算出来然后依次对内参进行求导,下面为了整洁忽略了变量的上标:
$$
\begin{aligned}
h(\boldsymbol{a}_k^S, \boldsymbol{\theta}^a) &= \boldsymbol{TK}(\boldsymbol{a}-\boldsymbol{b})\\
&= \begin{bmatrix}
1 & -\beta_{yz} & \beta_{zy} \\
0 & 1 & -\beta_{zx} \\
0 & 0 & 1
\end{bmatrix}\begin{bmatrix}
s_x & 0 & 0\\
0 & s_y & 0\\
0 & 0 & s_z
\end{bmatrix}
\begin{bmatrix}
a_x - b_x\\
a_y - b_y\\
a_z - b_z
\end{bmatrix}\\
&=\begin{bmatrix}
s_x & -\beta_{yz}s_y & \beta_{zy}s_z\\
0 & s_y & -\beta_{zx}s_z\\
0 & 0 & s_z
\end{bmatrix}\begin{bmatrix}
a_x - b_x\\
a_y - b_y\\
a_z - b_z
\end{bmatrix}\\
&= \begin{bmatrix}
s_x(a_x - b_x) -\beta_{yz}s_y(a_y - b_y) + \beta_{zy}s_z(a_z - b_z) \\
s_y(a_y - b_y) -\beta_{zx}s_z(a_z - b_z) \\
s_z(a_z - b_z)
\end{bmatrix}
\end{aligned}
$$
接下来只需要对内参求偏导即可:
$$
\begin{aligned}
\frac{\partial h}{\partial\boldsymbol{\theta}^a} &= \begin{bmatrix}
\frac{\partial h_1}{\partial\beta_{yz}} & \frac{\partial h_1}{\partial\beta_{zy}} & \frac{\partial h_1}{\partial\beta_{zx}} & \frac{\partial h_1}{\partial s_x} & \frac{\partial h_1}{\partial s_y} & \frac{\partial h_1}{\partial s_z} & \frac{\partial h_1}{\partial b_x} & \frac{\partial h_1}{\partial b_y} & \frac{\partial h_1}{\partial b_z} \\
\frac{\partial h_2}{\partial\beta_{yz}} & \frac{\partial h_2}{\partial\beta_{zy}} & \frac{\partial h_2}{\partial\beta_{zx}} & \frac{\partial h_2}{\partial s_x} & \frac{\partial h_2}{\partial s_y} & \frac{\partial h_2}{\partial s_z} & \frac{\partial h_2}{\partial b_x} & \frac{\partial h_2}{\partial b_y} & \frac{\partial h_2}{\partial b_z}\\
\frac{\partial h_3}{\partial\beta_{yz}} & \frac{\partial h_3}{\partial\beta_{zy}} & \frac{\partial h_3}{\partial\beta_{zx}} & \frac{\partial h_3}{\partial s_x} & \frac{\partial h_3}{\partial s_y} & \frac{\partial h_3}{\partial s_z} & \frac{\partial h_3}{\partial b_x} & \frac{\partial h_3}{\partial b_y} & \frac{\partial h_3}{\partial b_z}
\end{bmatrix} \\
&= \begin{bmatrix}
s_y(a_y - b_y) & s_z(a_z - b_z) & 0 & a_x - b_x & -\beta_{yz}(a_y - b_y) & \beta_{zy}(a_z - b_z) & -s_x & \beta_{yz}s_y & -\beta_{zy}s_z\\
0 & 0 & -s_z(a_z - b_z) & 0 & a_y - b_y & -\beta_{zx}(a_z - b_z) & 0 & -s_y & \beta_{zx}s_z\\
0 & 0 & 0 & 0 & 0 & a_z - b_z & 0 & 0 & -s_z
\end{bmatrix}\\
&= \left[\begin{matrix}
s_y(a_y - b_y) & s_z(a_z - b_z) & 0 \\
0 & 0 & -s_z(a_z - b_z)\\
0 & 0 & 0
\end{matrix}|\quad \boldsymbol{T}\mathrm{diag}(\boldsymbol{a}-\boldsymbol{b})\quad|-\boldsymbol{TK}\right]
\end{aligned}
$$
这样我们就可以计算出残差的雅可比矩阵,进一步求 $\boldsymbol{H}$ 矩阵然后进行优化了。
注:这里采用的误差模型为 A Robust and Easy to Implement Method for IMU Calibration without External Equipments 中的误差模型,实际使用需要根据自己假设的误差模型计算雅克比矩阵,不过思路大同小异。
优化方法标定陀螺仪内参
对于陀螺仪的内参,首先用优化方法标定标度因子和轴偏差,这里我们先不考虑零偏的影响,零偏在下一部分随机误差标定中再说明。不考虑零偏的情况下,这里我们要优化的参数为:
$$
\boldsymbol{\theta}^a = \begin{bmatrix}
\beta_{yz}^g & \beta_{zy}^g & \beta_{zx}^g & \beta^g_{xz} & \beta^g_{xy} & \beta^g_{yx} & s_x^g & s_y^g & s_z^g
\end{bmatrix}
$$
标定陀螺仪内参需要用到加速度计测量值作为参考真值,因此需要先标定好加速度计内参再标定陀螺仪。具体如下:
对于一次加速度计测量我们可以获取其得到的重力方向的分量 $\boldsymbol{u}_{a, k - 1}$, 在这之后旋转 IMU 获取 n 组角速度读数,并对角速度计求解 IMU 的姿态变化,并计算得到重力方向的分量:$\boldsymbol{u}_g = \Psi(\omega_i^S, \boldsymbol{u}_{a, k - 1})$,并且此时我们从加速度计测量值也可以得到一个重力分量:$\boldsymbol{u}_{a, k}$,通过这两个比较可以构建残差并进行 LM 优化:
$$
\boldsymbol{L}(\boldsymbol{\theta}^a) = \sum_{k = 1}^M(\boldsymbol{u}_{a, k} - \Psi(\omega_i^S, \boldsymbol{u}_{a, k - 1}))^2
$$
关于如何从离散角速度积分得到姿态变化,论文作者采用了四阶龙格库塔法,具体可以参考论文。
滤波方法
除了以上两种思路以外,还可以采用滤波的方法来标定误差。之后补上过程。
随机误差标定
在误差分析中,我们提到了除了标度因子和轴偏差以外,还有一部分我们没办法通过标定去除的误差,即测量值中的高斯白噪声以及对高斯白噪声积分得到的随机游走,这里面我们一般通过 Allan 方差对其不确定度进行确定。Allan 方差能够标定的误差不确定度包括:
- (角度/速度)随机游走
- (角速度/加速度)随机游走
- 零偏不稳定性
Allan 方差标定的原理主要是利用功率谱的一些相关知识,由于我也不太熟悉所以这里不做深入,只总结了以下标定过程和怎么获取标定结果。过程如下:
- 将 IMU 静置一段时间,先按照周期 T 采集一段数据,对这组数据可以计算出其方差
- 将采集到的数据每两个进行平均,相当于我们 以 2T 周期采集了另一组数据,同样可以计算出相应的方差
- 用同样的方法获取不同周期下的方差数据,绘制方差-周期曲线(log-log 形式)
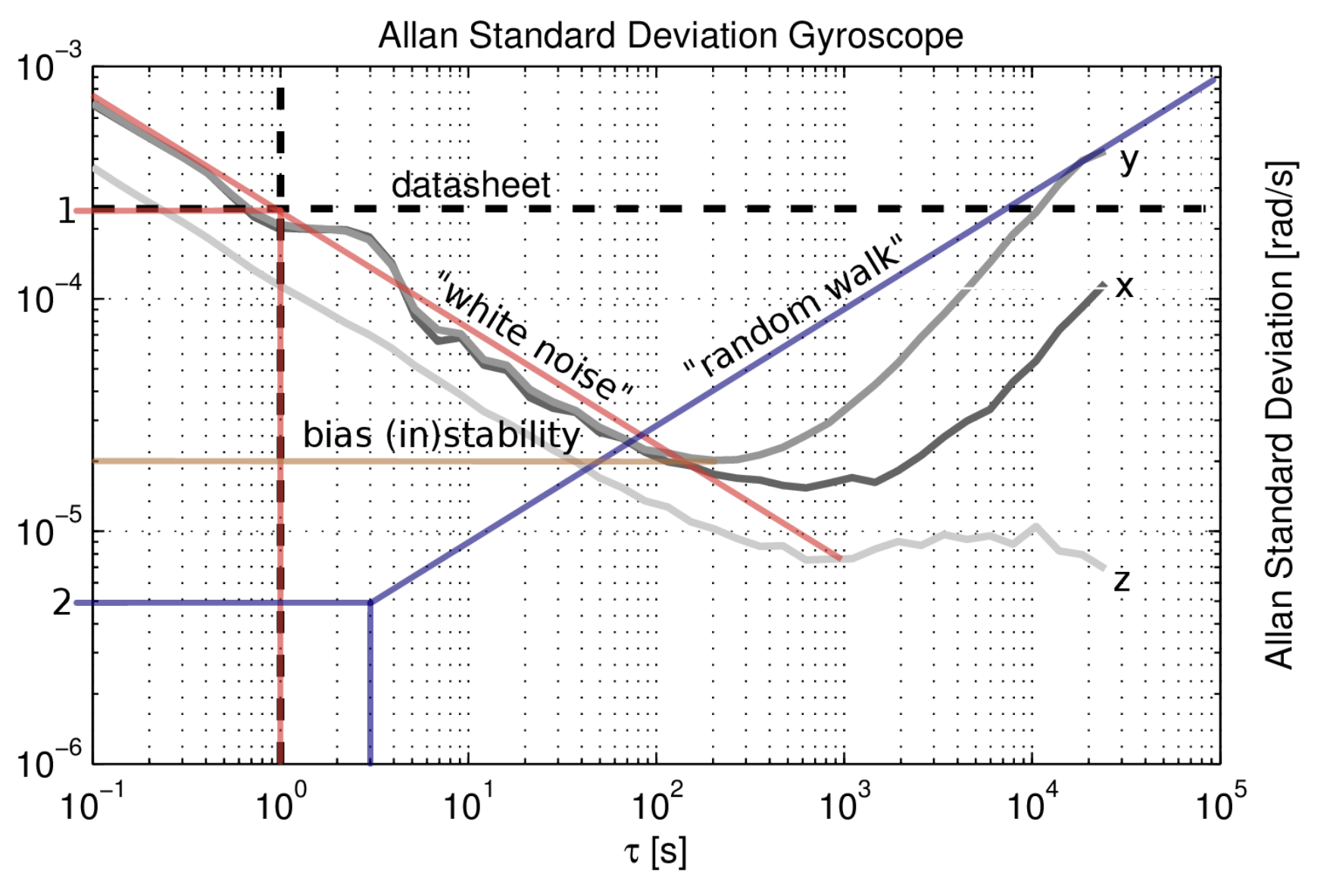
以下图为例,图中绘制 x, y, z 三个型号的陀螺仪的艾伦方差曲线
不确定度参数获取方式如下,找到下面各个参数对应的位置与 $\tau = 10^0 = 1$ 的交点,再将对应的 Y 值转化为对应的不确定度即可:
- 量化噪声(quantization noise):斜率为 -1,转换关系:
$y = \sqrt{3}Q$ - 白噪声/(角度/速度)随机游走(white noise/ (angle/velocity) random walk): 斜率为 -1/2,转换关系:
$y = N$ - 零偏不稳定性(bias instablity):斜率为 0(曲线最低点),转换关系:
$y = \frac{2B}{3}$ - (角速度/加速度)随机游走(angle velocity/acceralation random walk):斜率为 1/2,转换关系:
$y = \frac{K}{\sqrt{3}}$ - 速率斜坡(rate ramp):斜率为 1,转换关系:
$y = \frac{R}{\sqrt{2}}$