简介
IMU 里的误差主要来源于以下三个部分:零偏,尺度因子和轴偏差。下面分别进行说明:
零偏和噪声 Bias & Noise
首先只考虑零偏和噪声,以角速度为例,角速度的噪声模型如下所示:
$$
\begin{aligned}
\tilde{\omega}(t) &= \omega(t) + b(t) + n(t) \\
\dot{b}(t) &= n_b(t)
\end{aligned}
$$
其中,$b(t)$ 为零偏,零偏为传感器测量值和真实值的差值。例如当物体静止时,如果不考虑重力加速度的影响,加速度计输出应该为 0,但实际中可能会是一个很小的非零值,这个就是零偏,由于零偏是直接作用在加速度上的,因此当我们用加速度测量值来计算位置变化时,其影响对时间是二次的。$n(t)$ 是一个高斯白噪声,一个均值为 $0$,方差为 $\sigma$ 并且各时刻之间互相独立,同时可以看到零偏的导数也是一个高斯白噪声。高斯白噪声一阶矩(均值)为0,二阶距(协方差)随时间会发生变化,即:
$$
\begin{aligned}
E(n(t)) &\equiv 0 \\
E(n(t_1)n(t_2)) &= \sigma^2\delta(t_1-t_2)
\end{aligned}
$$
上式中,$\delta(t)$ 为狄拉克函数,如下所示:
$$
\delta(t) = \left\{
\begin{aligned}
+\infty \qquad t = 0 \\
0 \qquad t\neq 0
\end{aligned}
\right.
$$
表明不同时刻时间噪声相互独立,每个时刻的噪声服从均值为 $0$, 方差为 $\sigma$ 的高斯分布,$\sigma$ 越大表示噪声不确定度越大。
上面的模型我们考虑都是在时间连续的情况。而实际使用中,我们用的都是离散时间的采样,因此需要了解离散和连续高斯白噪声之间的关系,从而了解我们怎么对离散的噪声进行建模。在上述的角速度模型中,我们假设在采样时间内测量值是个常量,传感器在这段时间内测量值计算如下:
$$
\begin{aligned}
\frac{1}{\Delta t}\int_{t_0}^{t_0+\Delta t}{\tilde{\omega}}(t)dt &= \frac{1}{\Delta t}\int_{t_0}^{t_0+\Delta t}[\omega(t) + b(t) + n(t)]dt \\
\Rightarrow \tilde{\omega}(t_0+\Delta t)&= \omega(t_0 + \Delta t) + \frac{1}{\Delta t}\int_{t_0}^{t_0+\Delta t}\left[b(t) + n(t)\right]dt
\end{aligned}
$$
因此,除了真值部分以外,下面来考虑偏置和高斯白噪声对离散结果的影响,首先考虑高斯白噪声 $n(t)$ 的值和协方差:
$$
\begin{aligned}
n_d[k] \triangleq n(t_0 + \Delta t) &\approxeq \frac{1}{\Delta t}\int_{t_0}^{t_0+\Delta t}{n(\tau)}d\tau \\
E(n_d^2[k]) = \sigma_d^2 &= E\left(\frac{1}{\Delta t^2}\int_{t_0}^{t_0+\Delta t}\int_{t_0}^{t_0+\Delta t}{n(\tau)}n(t)d\tau dt\right) \\
利用期望性质&= \frac{1}{\Delta t^2}\int_{t_0}^{t_0+\Delta t}\int_{t_0}^{t_0+\Delta t}E(n(\tau)n(t))d\tau dt \\
&= \frac{\sigma^2}{\Delta t^2}\int_{t_0}^{t_0+\Delta t}\int_{t_0}^{t_0+\Delta t}\delta(t - \tau)d\tau dt \\
&= \frac{\sigma^2}{\Delta t^2}\int_{t_0}^{t_0+\Delta t} 1 dt \\
&= \frac{\sigma^2}{\Delta t^2}(\Delta t) \\
\sigma_d^2 &= \frac{\sigma^2}{\Delta t}
\end{aligned}
$$
上式协方差推导中,第一步到第二步利用了数学期望的性质将求期望移到积分内部,通过 $E(n(t_1)n(t_2)) = \sigma^2\delta(t_1-t_2)$ 进行代换,最后计算得到离散的白噪声的协方差和连续的白噪声的协方差的关系,可以发现模拟和离散量的不确定度之间存在一个 $\sqrt{\Delta t}$ 的比例关系,当我们用 $\sigma$ 的单位为 $\mathrm{deg/s}$, 则 $\sigma_d$ 的单位为$\mathrm{deg/(s^{3/2})}$。
接下来考虑零偏对离散采样造成的影响,上面我们对零偏建模假定其导数在连续时间内是一个高斯白噪声,因此对高斯白噪声的积分是一个一阶马尔科夫过程,计算经过采样时间后零偏的值及其协方差:
$$
\begin{aligned}
b(t_0 + \Delta t) &= b(t_0) + \int_{t_0}^{t_0+\Delta t}n_b(t)dt \\
E\{b^2(t_0 + \Delta t)\} &= E\left\{\left[b(t_0) + \int_{t_0}^{t_0+\Delta t}n_b(t)dt\right]\left[b(t_0) + \int_{t_0}^{t_0+\Delta t}n_b(t)dt\right]\right\} \\
&= E\left\{\left[b(t_0)^2 + 2b(t_0)\int_{t_0}^{t_0+\Delta t}n_b(t)dt + (\int_{t_0}^{t_0+\Delta t}n_b(t)dt)^2\right]\right\} \\
&= E{b(t_0)^2} + E\left\{2b(t_0)\int_{t_0}^{t_0+\Delta t}n_b(t)dt\right\} + E\left\{(\int_{t_0}^{t_0+\Delta t}n_b(t)dt)^2\right\} \\
&= E\{b(t_0)^2\} + 2b(t_0)\int_{t_0}^{t_0+\Delta t}E\{n_b(t)\}dt + E\left\{(\int_{t_0}^{t_0+\Delta t}n_b(t)dt)^2\right\} \\
&= E\{b(t_0)^2\} + E\{n_b(t)n_b(\tau))\} \\
&= E\{b(t_0)^2\} + \sigma_b^2\Delta t
\end{aligned}
$$
可以看出来,在离散时间内,每一时刻的零偏都是在上一时刻的零偏上叠加了一个高斯白噪声,其不确定度为 $\sigma_{bd} = \sigma_b\sqrt{\Delta t}$,单位是 $\mathrm{deg/(s^{3/2})}$,(因为零偏的导数的单位为: $\mathrm{deg/s^2}$)。对这种一阶马尔科夫性质的噪声称为随机游走,因此角速度中含有的这部分随机游走就是角速度随机游走。同理,由角速度积分得到的角度由于角速度的高斯白噪声同样会产生一个角度随机游走,角速度的不确定度单位为 $\mathrm{deg/s}$,因此角度随机游走的单位为: $\mathrm{deg/(s^{1/2})}$。
整理一下:对于 IMU 测量值(加速度、角速率)而言,噪声来源有:
- 测量值本身的高斯白噪声,不确定度单位为:
- 角速度:
$\mathrm{deg/(s^{3/2})}$,由角速度本身的单位除以$\sqrt{s}$得到 - 加速度:
$\mathrm{m/(s^{5/2})}$,由加速度的单位除以$\sqrt{s}$得到
- 角速度:
- 由零偏的一阶高斯白噪声积分得到的随机游走,不确定度单位为:
- 角速度:
$\mathrm{deg/(s^{5/2})}$,由零偏的导数(角加速度)本身的单位乘$\sqrt{s}$得到 - 加速度:
$\mathrm{m/(s^{5/2})}$,由零偏的导数的单位乘$\sqrt{s}$得到
- 角速度:
除此之外,零偏还有以下误差来源:
- 零偏重复性:多次启动时,零偏不相等,因此会有一个重复性误差。在实际使用中,需要每次上电都重新估计一次。
- 零偏不稳定性:零偏随时间缓慢变化,其变化值无法预估,需要假定一个概率区间描述它有多大的可能性落在这个区间内,一般通过角速度/加速度随机游走来衡量不确定度的大小
- 速率斜坡:通常由于温度引起的零位变化,可以通过温度补偿进行消除
尺度因子 Scale errors
尺度因子指传感器测量值和实际数值之间的比值,这个通常会由于单位转换导致的,比如我们将仪器中测的电信号转换为距离/角度信号等,会进行一个比例换算,而在这个过程比例因子不准确的话造成的误差也是成比例的,这个部分就是尺度因子。内参中一般用一个标度因数矩阵来表示,如下所示:
加速度标度因数矩阵:
$$
K^a = \begin{bmatrix}
s_x^a & 0 & 0 \\
0 & s_y^a & 0 \\
0 & 0 & s_z^a
\end{bmatrix}
$$
角速度标度因数矩阵:
$$
K^g = \begin{bmatrix}
s_x^g & 0 & 0 \\
0 & s_y^g & 0 \\
0 & 0 & s_z^g
\end{bmatrix}
$$
因此,真值与测量值的关系为:
$$
\begin{aligned}
\boldsymbol{a}^O &= \boldsymbol{K}^a\boldsymbol{a}^S\\
\boldsymbol{\omega}^O &= \boldsymbol{K}^g\boldsymbol{\omega}^S
\end{aligned}
$$
其中,上标 $O$ 表示真值,$S$ 表示传感器测量值。
轴偏差 Axis Misaligment
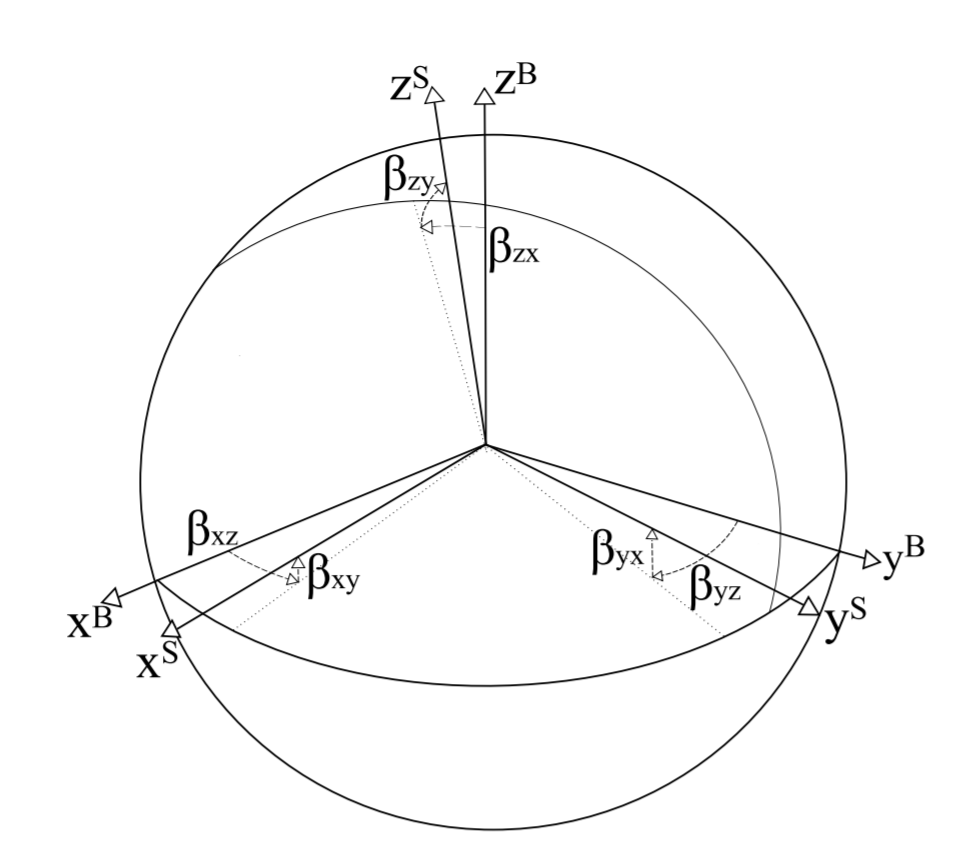
上面大部分都是对单独某个轴进行分析,但实际中我们使用的三轴器具都不是严格正交的,因此有轴偏差带来的误差,如下图所示:
通常用一个安装误差矩阵来表示,如下所示:
$$
\boldsymbol{T} =
\begin{bmatrix}
1 & -\beta_{yz} & \beta_{zy} \\
\beta_{xz} & 1 & -\beta_{zx} \\
-\beta_{xy} & \beta_{yx} & 1
\end{bmatrix}
$$
不考虑其他误差的情况下,真值与测量值的转换关系为:
$$
\begin{aligned}
\boldsymbol{a}^O = \boldsymbol{T}\boldsymbol{a}^O \\
\boldsymbol{\omega}^O = \boldsymbol{T}\boldsymbol{\omega}^O
\end{aligned}
$$
其中,上标 $O$ 表示真值,即理想的正交坐标系。$S$ 表示测量值,即不严格正交的传感器坐标系
总结
整合一下上面提到的三种误差,最后传感器测量值和真实值的关系可以表示为以下形式:
$$
\begin{aligned}
\boldsymbol{a}^O &= \boldsymbol{T}^a\boldsymbol{K}^a(\boldsymbol{a}^S + \boldsymbol{b}^a + \boldsymbol{n}^a) \\
\boldsymbol{\omega}^O &= \boldsymbol{T}^\omega\boldsymbol{K}^\omega(\boldsymbol{\omega} + \boldsymbol{b}^a + \boldsymbol{n}^a)
\end{aligned}
$$