简介
前置知识
在学习 IMU,首先需要了解对运动的物体而言,其在不同坐标系下的区别和联系。
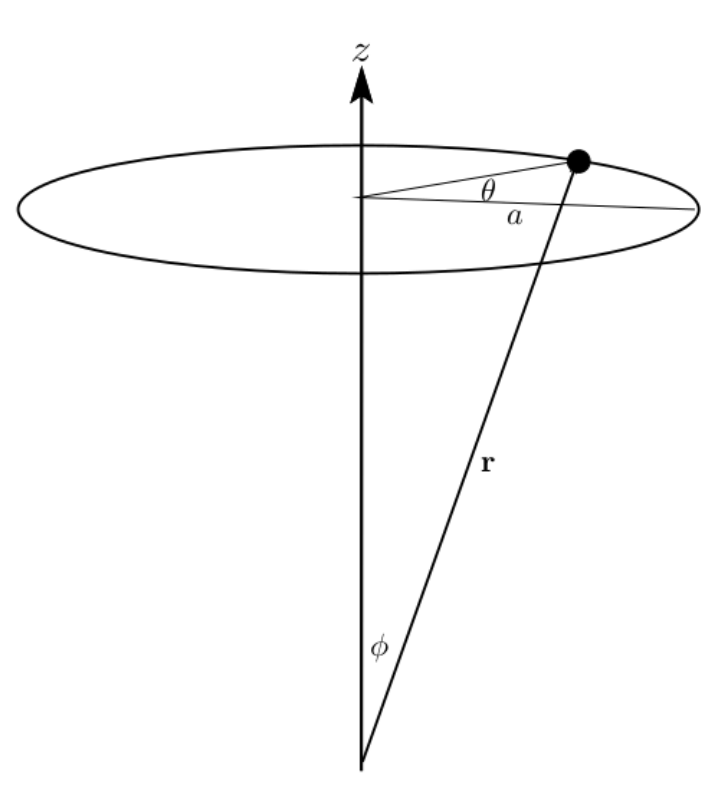
- 简单的圆周运动
以上图为例,一个点在高度为 $h$ 的平面做以 $a$ 为半径的圆周运动,它的坐标函数为: $\boldsymbol{r} = (a\cos{\theta}, a\sin{\theta}, h)^\mathrm{T}$,对该运动坐标求导可得其速度:
$$
\begin{aligned}
\dot{\boldsymbol{r}} &= (-a\dot{\sin{\theta}}, a\dot{\cos{\theta}}, 0)^\mathrm{T} \\
\mathrm{矩阵分解} &= \begin{bmatrix}
0 & -\dot{\theta} & 0\\
\dot{\theta} & 0 & 0\\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
a\cos{\theta} \\
a\sin{\theta} \\
h
\end{bmatrix} \\
&= \boldsymbol{w} \times \boldsymbol{r} = \boldsymbol{\omega}^\wedge\boldsymbol{r}
\end{aligned}
$$
上式化简结果可以看出来点的角速度为 $\boldsymbol{\omega} = \dot{\theta}\boldsymbol{z}$, $|\dot{\theta}|$ 是角速度的大小,线速度的大小计算如下:
$$
|\dot{\boldsymbol{r}}| = |\boldsymbol{\omega}||\boldsymbol{r}|\sin{\phi}=a|\dot{\theta}|
$$
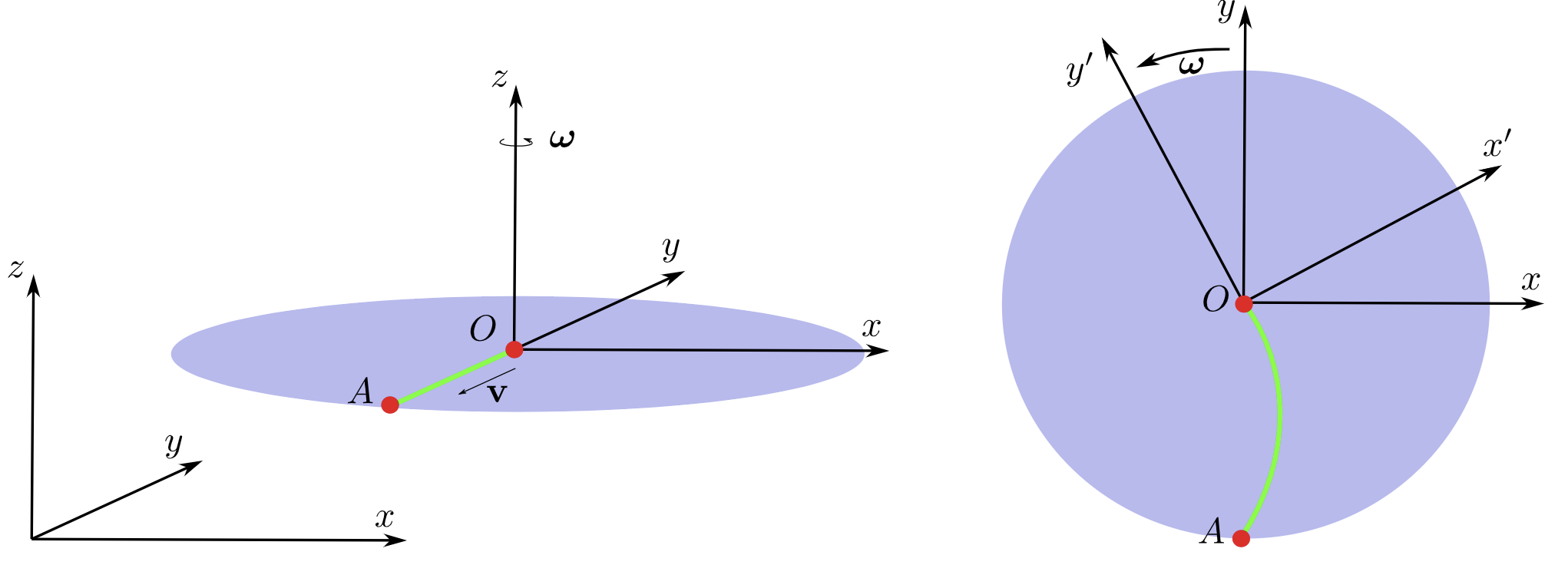
- 圆周运动和匀速运动结合
之前的例子比较简单,接下来来看一个复杂的例子。这个例子中,光滑的圆盘本身以 $\boldsymbol{\omega}$ 的角速度在做圆周运动,一个粒子从圆盘圆心向一个方向进行匀速运动至圆盘边缘。这个时候我们可以考虑一下在不同坐标系下粒子运动的轨迹。图中一个涉及两个坐标系:世界坐标系(惯性系)和圆盘坐标系。其中圆盘坐标系固定在圆盘上并随圆盘一起转动。
对于世界坐标系而言,由于圆盘是光滑的所以粒子的运动不会受其干扰,所以显然粒子的轨迹是一条从圆心延申至边缘的直线;而对于圆盘坐标系而言,粒子在做一个匀速直线运动和角速度为 $-\boldsymbol{\omega}$ 的圆周运动叠加的复合运动,所以不难想象,在圆盘坐标系下,粒子的轨迹是向外发散的弧线(半径逐渐变大的圆周运动)。定性来分析的话,假定粒子距圆心距离的距离为为 $r(t)$ (匀速直线运动),旋转角度(粒子与圆心连线和 $x$ 轴正方向的夹角)为 $-\theta(t)$(因为和圆盘的旋转方向相反),粒子的坐标函数(轨迹)为:
$$
\begin{aligned}
\boldsymbol{p} &= (r(t)\cos{-\theta(t)}, r(t)\sin{(-\theta(t))}) \\
&= (r(t)\cos{(\theta(t))}, -r(t)\sin{(\theta(t))})
\end{aligned}
$$
- 考虑坐标系之间的转换关系
上面我们以一个例子简单分析了物体运动时在世界坐标系(惯性系 i)和圆盘坐标系(旋转坐标系)体现出来的轨迹的区别,这里我们分析一下一个运动的物体在一个旋转坐标系(通常是一个物体,因此这里用 body 系 b 来指代)和一个惯性系下速度(分别为 $\boldsymbol{v}^b$ 和 $\boldsymbol{v}^i$)的关系。
考虑一个旋转坐标系在世界坐标系下的旋转矩阵为 $\boldsymbol{R_{ib}}$ (不考虑平移),一个质量块在旋转系下的坐标为 $\boldsymbol{r}^b(t) = (x_1, x_2, x_3)^\mathrm{T}$,其在惯性系下的坐标显然为: $\boldsymbol{r}^i = \boldsymbol{R}_{ib}\boldsymbol{r}^b$,对时间求导为:
$$
\begin{aligned}
\dot{\boldsymbol{r}}^i &= \boldsymbol{R}_{ib}\dot{\boldsymbol{r}}^b + \dot{\boldsymbol{R}_{ib}}\boldsymbol{r}^b \\
旋转矩阵求导&= \boldsymbol{R}_{ib}\dot{\boldsymbol{r}}^b + \boldsymbol{R}_{ib}\boldsymbol{\omega}^b_\times\boldsymbol{r}^b \\
叉乘性质&= \boldsymbol{R}_{ib}\dot{\boldsymbol{r}}^b + (\boldsymbol{R}_{ib}\boldsymbol{\omega}^b)_\times\boldsymbol{R}_{ib}\boldsymbol{r}^b \\
坐标转换 &= \boldsymbol{R}_{ib}\dot{\boldsymbol{r}}^b + (\boldsymbol{R}_{ib}\boldsymbol{\omega}^b)_\times\boldsymbol{r}^i\\
\boldsymbol{v}^i &= \boldsymbol{R}_{ib}\boldsymbol{v}^b + \boldsymbol{\omega}_\times \boldsymbol{r}^i\\
\Rightarrow \boldsymbol{R}_{ib}\boldsymbol{v}^b &= \boldsymbol{v}^i - \boldsymbol{\omega}_\times \boldsymbol{r}^i
\end{aligned}
$$
上式中关于旋转矩阵求导可以参考我的上一篇博客。这里我们可以看到:用旋转矩阵 $\boldsymbol{R}_{ib}$ 直接对 $\boldsymbol{v}^b$ 进行转换不能直接得到 $\boldsymbol{v}^i$ 中间还有一个由旋转造成的差值。
推导了不同坐标系直接速度的转换关系,下面进一步进行加速度的推导:
$$
\begin{aligned}
\ddot{\boldsymbol{r}} = \boldsymbol{a}^i &= \boldsymbol{R}_{ib}\dot{\boldsymbol{v}}^b + \dot{\boldsymbol{R}_{ib}}\boldsymbol{v}^b + (\boldsymbol{R}_{ib}\boldsymbol{\omega}^b)'_\times\boldsymbol{r}^i + (\boldsymbol{R}_{ib}\boldsymbol{\omega}^b)_\times\dot{\boldsymbol{r}^i} \\
&= \boldsymbol{R}_{ib}\boldsymbol{a}^b + \dot{\boldsymbol{R}_{ib}}\boldsymbol{v}^b + (\boldsymbol{R}_{ib}\boldsymbol{\omega}^b)'_\times\boldsymbol{r}^i + \boldsymbol{\omega}_\times\boldsymbol{v}^i \\
&= \boldsymbol{R}_{ib}\boldsymbol{a}^b + \dot{\boldsymbol{R}_{ib}}\boldsymbol{v}^b +\boldsymbol{\omega}_\times(\boldsymbol{R}_{ib}\boldsymbol{v}^b + \boldsymbol{\omega}_\times \boldsymbol{r}^i) + (\boldsymbol{R}_{ib}\boldsymbol{\omega}^b)'_\times\boldsymbol{r}^i \\
用 \boldsymbol{v} 表示 \boldsymbol{R}_{ib}\boldsymbol{v}^b &= \boldsymbol{R}_{ib}\boldsymbol{a}^b + \dot{\boldsymbol{R}_{ib}}\boldsymbol{v}^b +\boldsymbol{\omega}_\times(\boldsymbol{v} + \boldsymbol{\omega}_\times \boldsymbol{r}^i) + (\boldsymbol{R}_{ib}\boldsymbol{\omega}^b)'_\times\boldsymbol{r}^i \\
&= \boldsymbol{R}_{ib}\boldsymbol{a}^b + \dot{\boldsymbol{R}_{ib}}\boldsymbol{v}^b +\boldsymbol{\omega}_\times(\boldsymbol{v} + \boldsymbol{\omega}_\times \boldsymbol{r}^i) + (\dot{\boldsymbol{R}}_{ib}\boldsymbol{\omega}^b + \boldsymbol{R}_{ib}\dot{\boldsymbol{\omega}}^b)_\times\boldsymbol{r}^i
\end{aligned}
$$
上式中,$\dot{\boldsymbol{R}}_{ib}\boldsymbol{\omega}^b = \boldsymbol{R}_{ib}\boldsymbol{\omega}^b_\times\boldsymbol{\omega}^b$ 后两项为向量于自身叉乘为零,因此这项可以直接去掉,继续推导:
$$
\begin{aligned}
\ddot{\boldsymbol{r}} = \boldsymbol{a}^i &= \boldsymbol{R}_{ib}\boldsymbol{a}^b + \dot{\boldsymbol{R}_{ib}}\boldsymbol{v}^b +\boldsymbol{\omega}_\times(\boldsymbol{v} + \boldsymbol{\omega}_\times \boldsymbol{r}^i) + (\boldsymbol{R}_{ib}\dot{\boldsymbol{\omega}}^b)_\times\boldsymbol{r}^i \\
&= \boldsymbol{R}_{ib}\boldsymbol{a}^b + \boldsymbol{\omega}_\times\boldsymbol{R}_{ib}\boldsymbol{v}^b +\boldsymbol{\omega}_\times(\boldsymbol{v} + \boldsymbol{\omega}_\times \boldsymbol{r}^i) + (\boldsymbol{R}_{ib}\dot{\boldsymbol{\omega}}^b)_\times\boldsymbol{r}^i \\
&= \boldsymbol{R}_{ib}\boldsymbol{a}^b + \boldsymbol{\omega}_\times\boldsymbol{v} +\boldsymbol{\omega}_\times(\boldsymbol{v} + \boldsymbol{\omega}_\times \boldsymbol{r}^i) + \dot{\boldsymbol{\omega}}_\times\boldsymbol{r}^i \\
&= \boldsymbol{a} + 2\boldsymbol{\omega}_\times\boldsymbol{v} +\boldsymbol{\omega}_\times(\boldsymbol{\omega}_\times \boldsymbol{r}^i) + \boldsymbol{\alpha}_\times\boldsymbol{r}^i \\
\Rightarrow \boldsymbol{a} &= \boldsymbol{a}^i - 2\boldsymbol{\omega}_\times\boldsymbol{v} - \boldsymbol{\omega}_\times(\boldsymbol{\omega}_\times \boldsymbol{r}^i) - \boldsymbol{\alpha}_\times\boldsymbol{r}^i \\
\end{aligned}
$$
上面推导的第二到第三步我们同样用到了旋转矩阵求导的另一个性质 $\dot{\boldsymbol{R}} = \boldsymbol{\omega}\boldsymbol{R}$ 这里的 $\boldsymbol{\omega} = \boldsymbol{R}_{ib}\boldsymbol{\omega}^i$, 表示这个旋转矩阵对应的角速度在 i 系下的表达。
此外,上式的结果中,对于物体运动在不同坐标系下的表示,我们用了三种表示方式,以速度为例,分别是:
$\boldsymbol{v}^i$:物体相对于 i 系的速度$\boldsymbol{v}^b$: 物体相对于 b 系下的速度$\boldsymbol{v} = \boldsymbol{R}_{ib}\boldsymbol{v}^b$: 物体相对于 b 系的速度在 i 系下的表达,要和$\boldsymbol{v}^i$区分开
此外,还要注意区分,式中不同变量对应的主体:$\boldsymbol{p}, \boldsymbol{v}, \boldsymbol{a}$ 分别对应的是物体的位置,速度,加速度;而 $\boldsymbol{\omega}, \boldsymbol{\alpha}$ 则是对应旋转坐标系 b 的角速度和角加速度
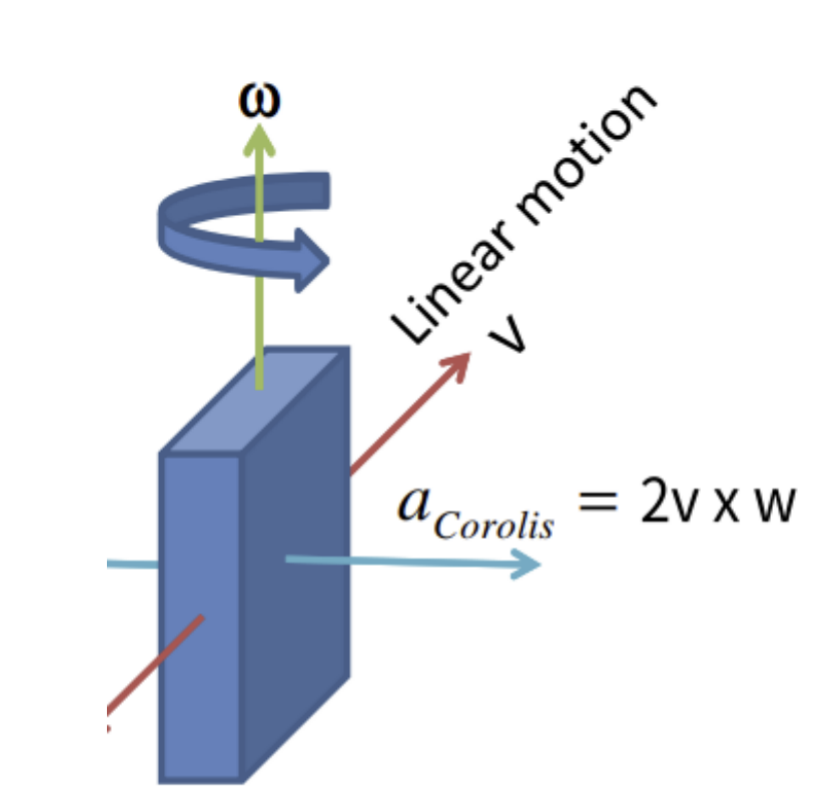
最后来看一下这个式子,其表示的是:在转换物体在 b 系的加速度至 i 系时,除了直接用旋转矩阵转换外,还额外受到了三个其他作用力的影响,分别是:
$2\boldsymbol{\omega}_\times\boldsymbol{v}$: 科式力,与 b 系角速度和物体速度有关,其方向与物体速度方向和 b 系角速度方向垂直。$\boldsymbol{\alpha}_\times\boldsymbol{r}^i$: 欧拉力,与 b 系角加速度和物体位置有关$\boldsymbol{\omega}_\times(\boldsymbol{\omega}_\times\boldsymbol{r}^i)$: 离心力,与 b 系角速度和物体位置有关
IMU 测量模型和运动模型
在了解了上述基础知识之后,接下来了解一下 IMU 的具体测量模型,分别为加速度计部分以及角速度部分。
加速度计工作原理
IMU 对于加速度的测量模型可以用一个质量块+弹簧+指示计模型来进行简化,如下图所示。
加速度计的测量值为 $\boldsymbol{a}_m$ 为弹簧拉力对应的测量值,即:$\boldsymbol{a}_m = \boldsymbol{f}/ m = \boldsymbol{a} - \boldsymbol{g}$,式中 $\boldsymbol{a}$ 为物体(IMU)在惯性系中的加速度,$\boldsymbol{g}$ 为重力加速度。
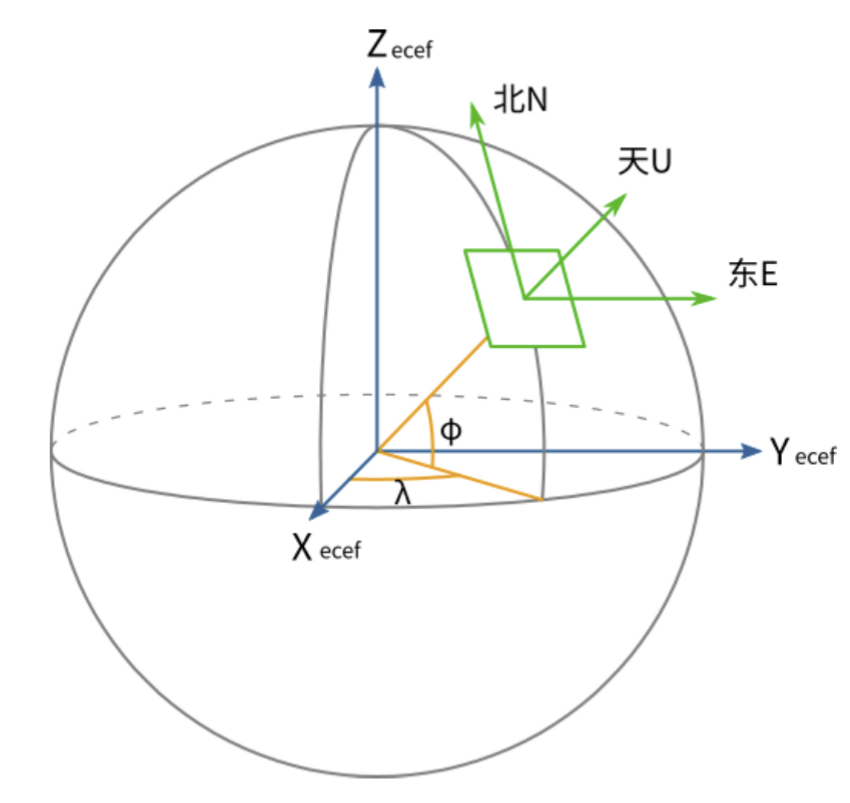
由于其中涉及到了重力加速度,因此我们需要引入一个新的坐标系,即东北天坐标系(East North Up, ENU),如下图所示,在地球的某一个位置,沿纬度方向指向东边为 $x$ 轴正方向,沿经度方向指向北边为 $y$ 轴正方向, 与地球秋心连线指向上(天空)为 $z$ 轴正方向。这个坐标系也经常被用来作为局部坐标系,其平面正切于地球表面。图中的另一个固定在球心的坐标系为地心地固坐标系(Earth-Centered,Earth-Fixed, ECEF)坐标系,其原点为地球质心, $x$ 轴指向本初子午线与赤道的交点,$y$ 轴垂直于xOz平面(即东经90度与赤道的交点), $z$ 轴指向北极点。
在 ENU 坐标系下,重力加速度为:$\boldsymbol{g} = (0, 0, -9.81)^\mathrm{T}$,假定 IMU 坐标系与 ENU 坐标系重合,当 IMU 静止时,有:$\boldsymbol{a} = 0, \boldsymbol{a}_m = -\boldsymbol{g}$;当 IMU 自由落体时,有:$\boldsymbol{a} = \boldsymbol{g}, \boldsymbol{a}_m = 0$。可以看到由于受重力加速度的影响,IMU 的测量值并不直接反映其本身的加速度,还要考虑重力的影响,并且其测量的加速度的坐标是在 Body 系下表示的,与世界坐标系之间存在一个旋转关系。
陀螺仪测量原理
陀螺仪用于测量物体的旋转角速度,目前使用的主要分为振动陀螺和光纤陀螺。
- 光纤陀螺
光纤陀螺的工作原理大致如上图所示:由一个光源发出入射光,经过分束镜后一束通过分束镜从右侧的的透镜进入光纤线圈经顺时针旋转至下侧的透镜出射再通过分束镜进入检测器;由光源发出的另一束光则被分束镜反射进入下侧的分束镜进入光纤线圈经逆时针旋转从右侧的透镜射出再被分束镜反射进入检测器。两束光在会和的时候会进行干涉,惯性器件没有旋转的时候两束光光程是一致的,而当惯性器件相对于惯性系发生旋转时,根据 Sagnac效应 两束光会产生一个光程差,通过这个光程差,我们可以计算出惯性器件旋转的角速度。
- 振动陀螺 MEMS
其中,振动陀螺时通过测量科式力来间接测量 IMU 的角速度。在上一部分中,我们已经知道在旋转坐标系中运动的物体会受到科式力的影响,而科式力与物体相对于旋转坐标系的速度与旋转坐标系本身的角速度有关。因此,如果我们将 IMU 看作旋转坐标系,并知道其中一个物体相对于 IMU 的速度其所受的科式力,我们就能计算出 IMU 的角速度了。
以下图为例,
在陀螺仪中,让一个质量块沿主动轴方向以一定速度 $v$ 进行运动,此时由于物体会受到科式力作用,因此我们在其运动方向和测量的角速度方向垂直的方向进行测量,能够得到一个科式力对应的角速度,而由于物体的运动速度已知,因此可以通过计算得出 IMU 再该轴的角速度。(实际中物体应该还受到离心力和欧拉力的影响,但由于物体里 IMU 坐标系与原点距离小,其影响投影在科式力方向的部分忽略不计)。
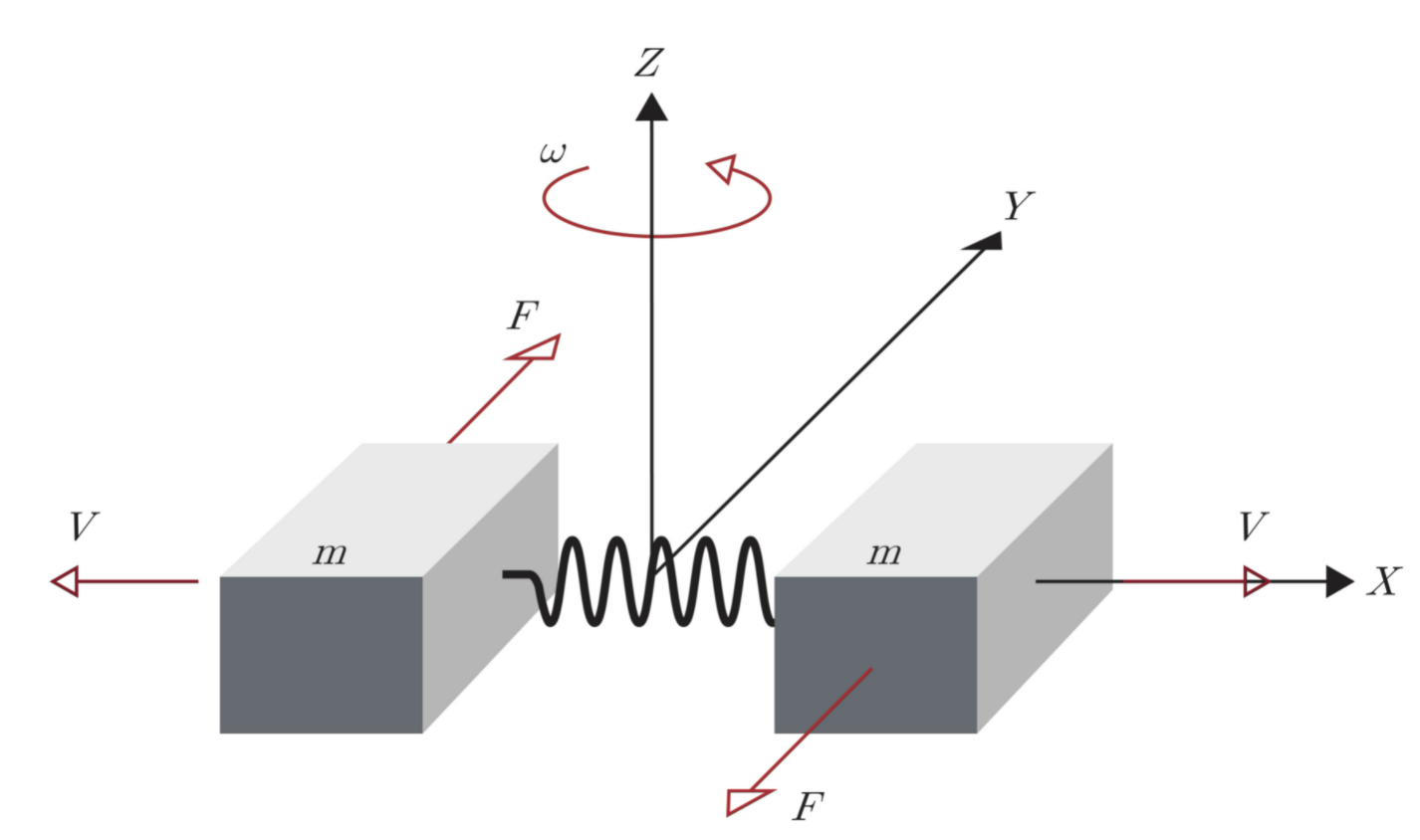
但这是假设 IMU 没有进行运动的情况下,如果 IMU 在科式力方向也在进行非匀速运动的话,我们测量的加速度值就会受 IMU 本身加速度的影响。因此为了消除这个影响,IMU 内部的测量模型如下图所示, 通过让两个质量块进行相反方向的运动,并对科式力方向进行测量,假设外部加速度为 $a_f$,不难发现其中一个结果:$a_f + a_c$,另一个为 $a_c - a_f$,通过简单的相减就可以将其影响消除掉。
当然实际上,两个质量块的质量不可能完全一致,因此这里会引入一个额外的误差,这个在后面的误差模型中会介绍。
IMU 误差模型
IMU 中加速度计和陀螺仪中的误差可以分为确定性误差和随机误差,其中确定性误差可以通过标定来确定其大小,而随机性误差则只能通过标定来判断其不确定度。
确定性误差中包括 Bias 和 Scale。Bias 为传感器测量的偏置,即传感器测量值和真实值的差值。例如当物体静止时,如果不考虑重力加速度的影响,加速度计输出应该为 0,但实际中可能会是一个很小的非零值,这个就是偏置,而由于这个偏置是直接作用在加速度上的,因此当我们用加速度测量值来计算位置变化时,其影响对时间是二次的。Scale 指传感器测量值和实际数值之间的比值,这个通常会由于单位转换导致的,比如我们将仪器中测的电信号转换为距离/角度信号等,会进行一个比例换算,而在这个过程比例因子不准确的话造成的误差也是成比例的,这个部分就是 scale。实际中这两种会误差会综合作用于测量值。
六面法标定加速度
将加速度计的3个轴分别朝上或者朝下水平放置一段时间,采集6个面的数据,此时我们都知道理论上的真实值(某一轴的值为重力加速度,另外两个轴为 0),因此和测量值进行比较,可以完成标定。
六面法标定陀螺仪
加速度计我们利用重力加速度 $\boldsymbol{g}$ 可以作为真实值来进行标定。在陀螺仪中,我们可以通过一个高精度转台来提供真实值,对各个轴分别进行顺时针和逆时针旋转来获取测量值,并和真实值作比较进行标定。
温度相关参数标定
同样的思路,利用恒温室来控温提供真实温度值,因为不同温度对误差造成的影响不是一样的,因此需要在一系列温度值下计算 bias 和 scale,最后绘制曲线作为标定结果。
随机误差标定————艾伦方差标定
标定大致流程为:
- 保持传感器绝对静止
- 对数据按时间进行分段,设定每个时间段的时长
- 讲传感器数据按照时间段进行平均
- 计算方差,绘制艾伦曲线
TODO;补充具体过程