简介

论文地址见：Robust and Precise Vehicle Localization based on Multi-sensor Fusion in Diverse City Scenes

这篇论文中，作者提出了一种框架可以融合 Lidar, RTK, IMU等传感器输入使汽车在复杂的城市和高速道路中进行稳定定位。主要贡献包括：

• 一个主动融合 Lidar, RTK, IMU 的定位框架
• 通过将 Lidar 中获得的反射值和高度值来在不同场景下得到稳定的状态估计结果
• 在不同场景下，如城市中心，高速和隧道进行了测试，保证定位有较好的结果

相关工作

多传感器融合方面的工作：

• INS/GPS/LiDAR integrated navigation system for urban and indoor environments using hybrid scan matching algorithm - 2D 激光雷达融合 GNSS, IMU
• Long-range GPS-denied aerial inertial navigation with LIDAR localization - Lidar 融合惯性导航，使用惯性导航作为里程计估计帧间位姿变换

基于 Lidar 的定位方面的工作：

• Map-Based Precision Vehicle Localization in Urban Environments - Thrun 大佬的工作，主要是基于 Lidar 反射值来进行建图和定位。

Lidar 地图构建

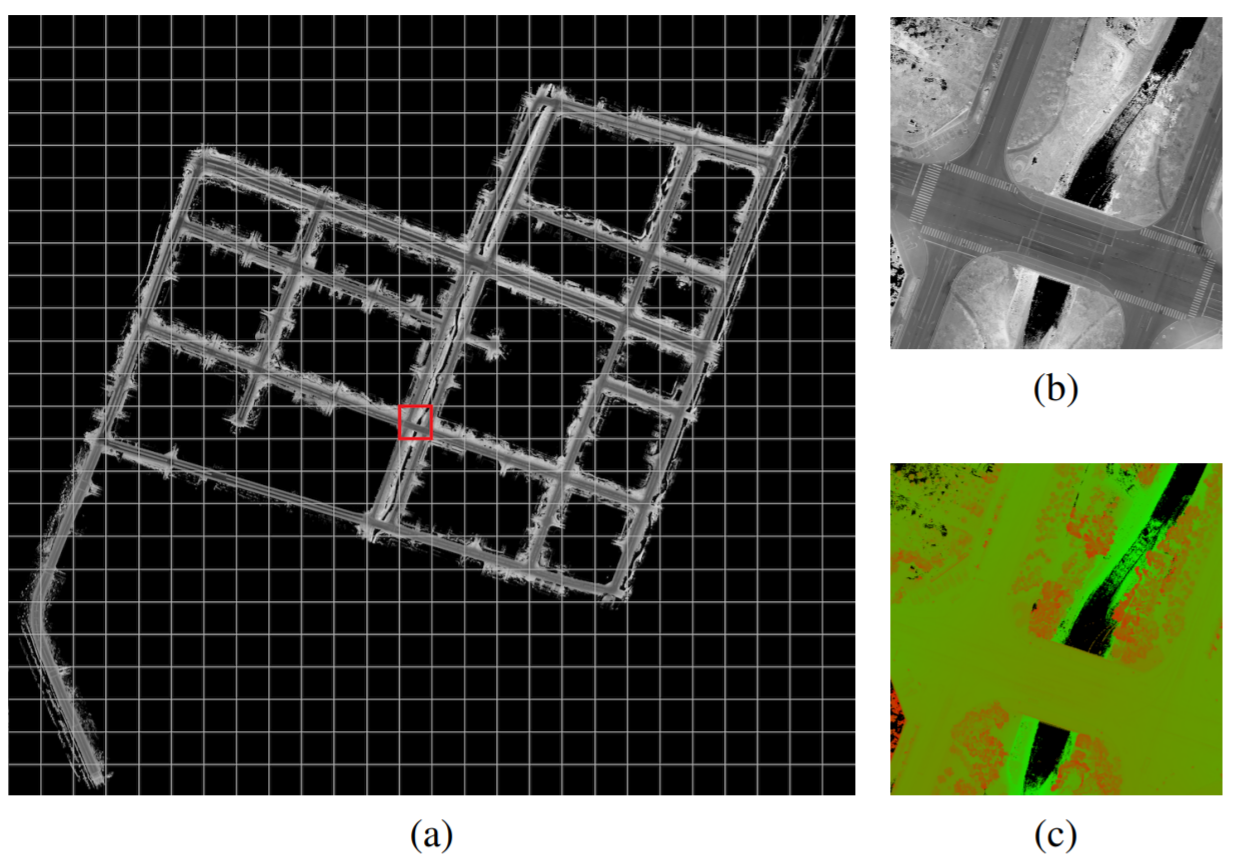
下一部分提到的定位算法依赖于一个先验地图，这一小节主要概括这个地图是怎么产生，作者使用的地图是基于栅格的地图，每个栅格中使用 Lidar 反射值（Intenstiy）和高度值来进行高斯分布的建模。下图展示了地图中反射值和高度值部分的具体例子：

基于 Lidar 的定位

论文中提出的定位系统对载体的位置、速度和姿态进行联合估计，具体包括：$(x, y, a, h)$。其中 $(x, y)$ 是投影平面（如 UTM 投影）的 2d 笛卡尔坐标，高度值 $a$ 则是通过和汽车的高度差来进行估计（假设汽车是平面上运动）。具体的方法是先基于 LK 算法估计姿态 $h$，在结合直方图滤波来估计水平坐标 $(x, y)$。以下为整体算法过程：

接下来会详细介绍各部分算法

偏航角 （yaw）估计

首先将在线点云投影至地面上，为了偏航角过程尽量高效，投影的时候进行了下采样，然后通过将投影点云和预先建立好的地图比较可以获得反射值和高度值的偏差和。这里论文作者将投影点云和先验地图作为两个图像，利用 LK 光流沿着梯度方向搜索可以最小化这两个误差。并且对这两个误差的处理稍有不同，对反射值误差作者使用了 Huber 鲁棒核函数来抑制异常点的影响，且对投影到亚像素级的点降低了权重，对高度值的误差则没有特别处理。在实现上，作者将这两种误差按一定权重结合，采用高斯牛顿法实现了一个多层光流，可以达到 1 度以内的准确度。值得注意的是，光流法本身也可以获得水平方向的定位，但作者没有光流得到结果，原因是水平定位精度不够高。

水平定位

系统采用直方图滤波来进行水平方向的定位。直方图滤波通过将状态空间分解成无数个区域并对每个区域估计一个概率值来估计后验概率。其预测和更新方程如下：

$$
\begin{aligned}
\bar{P}_{k, t} &= \sum_i P(X_t = x_k|u_t, X_{t-1} = x_i)P_{i, t-1}\\
P_{k, t} &= \eta P(z_t|X_t = x_k)\bar{P}_{k, t}
\end{aligned}
$$

上式中，$P_{k,t}$ 表示 $x_k$ 在 $t$ 时刻的置信值，$u_t$ 是控制输入，$z_t$ 是观测向量。在本文求解的问题中，状态值为 $(x, y)$。观测值为 Lidar 反射值和高度值。

首先来看预测阶段：预测阶段是在上一时刻分布上通过施加控制变量来预测当前分布。这里作者使用的是惯导 SINS 获得运动估计，并以此对进行预测，且用高斯变量的随机游走来更新分布的协方差，因此预测方程如下：

$$
\bar{P}(x, y) = \eta \sum_{i, j}P(i, j)\exp{(-\frac{(i - x)^2 + (j - y)^2}{2\sigma^2})}
$$

式中，$\bar{P}(x, y)$ 表示预测概率分布，$P(i, j)$ 表示通过 SINS 更新后的某一个状态区域的概率，$\sigma$ 是用来表示两帧之间漂移的参数。

接下来看更新阶段：预测阶段是用观测值来获得每个状态的后验概率，参考以下方程：

$$
P(x, y|z, m) = \eta P(z|x, y, m)(\bar{P}(x, y))^{1/\kappa}
$$

式中，$z$ 式通过点云构建的在线地图，$m$ 是先验雷达地图。$(x, y)$ 是运动位姿，$\kappa$ 是用来描述 $\sum_{xy}P(z|x,y,m)$ 和 $\sum_{xy}\bar{P}(x, y)$ 两个分布之间差异性的 KL 散度。这里作者不考虑 GNSS/IMU 带来的不确定度，这个会在后面部分通过另一种方式实现更好的融合。下面来看这两个分布如何计算。

对于 $P(z|x, y, m)$ 计算方式是将在线点云和先验地图比较，残差项为反射值和高度值的加权结合：

$$
P(z|x,y,m) = \eta P(z_r|x, y, m)^{\gamma}P(z_a|x, y, m)^{1-\gamma}
$$

式中，$z_r, z_a$ 分别表示传感器的反射值和高度值的观测。反射值使用离差平方和 SSD (Sum of Squared Difference) 构建残差如下：

$$
\text{SSD}_r = \sum_{i, j}\frac{(r_{m_{i - x, j - y}}-r_{z_{i,j}})^2(\sigma^2_{m_{i-x,j-y}} + \sigma^2_{z_{i,j}})}{\sigma^2_{m_{i-x,j-y}}\sigma^2_{z_{i,j}}}
$$

式中，$r_m, r_z$ 分别表示先验地图和在线点云中在某个栅格下的平均反射值。$\sigma_m, \sigma_z$ 则是对应的反射值标准差。这里将标准差引入引入可以降低环境变化的影响。（如果两个反射值差异很大，但是其方差都很小，则表示环境可能出现了变化。）

同理，用 SSD 来计算高度值的残差：

$$
\text{SSD}_a = \sum_{i, j}(a_{m_{i - x, j - y}}-a_{z_{i,j}})^2
$$

这里，没有考虑标准差是因为高度方向上天然会存在变化。在计算出残差之后，两个观测分布通过定义如下，其中 $\alpha = e$ 时为高斯分布，通过调整 $\alpha$ 可以调整平滑性：

$$
\begin{aligned}
    P(z_r|x, y, m) &= \eta \alpha^{-\frac{\text{SSD}_r}{2N_z}}\\
    P(z_a|x, y, m) &= \eta \alpha^{-\frac{\lambda\text{SSD}_a}{2N_z}}\\
\end{aligned}
$$

在更新过程中，权重因子 $\gamma$ 起到比较大的调整作用，论文中作者根据两个观测的分布的协方差来自动调整权重。两个观测分布 $[P(z_r|x, y, m)]_{xy}, [P(z_a|x, y, m)]_{xy}$ 的在两个方向上的方差定义如下：

$$
\begin{aligned}
    \sigma^2_x &= \frac{\sum_{xy}P(x, y)^\beta(x-\bar{x})^2}{\sum_{xy}P(x,y)^\beta}\\
    \sigma^2_x &= \frac{\sum_{xy}P(x, y)^\beta(y-\bar{y})^2}{\sum_{xy}P(x,y)^\beta}
\end{aligned}
$$

通过上述公式计算出两个观测分布在 $x,y$ 方向上的方差后，权重因子计算如下：

$$
\begin{aligned}
\gamma &= \frac{\sigma^2_x(a)\sigma^2_y(a)}{\sigma^2_x(a)\sigma^2_y(a) + \sigma^2_x(r)\sigma^2_y(r)}\\
    &= \frac{1}{1 + \frac{\sigma^2_x(r)\sigma^2_y(r)}{\sigma^2_x(a)\sigma^2_y(a)}}
\end{aligned}
$$

回顾以下两个观测的融合公式：

$$
P(z|x,y,m) = \eta P(z_r|x, y, m)^{\gamma}P(z_a|x, y, m)^{1-\gamma}
$$

不难发现，当反射值的不确定度越大，其权重会越小。通过这样可以将信息尽量集中在观测置信度较高的部分。

在更新阶段结束之后，下一步是决定最优位姿：这里作者没有使用所有直方图滤波中所有状态来估计最优位姿，而是只使用后验概率值最大或第二大的状态的周围一小范围区域。如果后验概率值第二大的状态其概率值超过最大后验概率状态的一定比例，且更靠近后验概率分布的中心，那么使用第二大的状态，否则使用后验概率最大的状态。假设该范围为 $\mathcal{Z}$，最优运动估计 $(\tilde{x}, \tilde{y})$ 计算如下：

$$
\begin{aligned}
    \tilde{x} &= \frac{\sum_{(x, y)\in \mathcal{Z}})P(x, y)^\beta x}{\sum_{(x, y)\in\mathcal{Z}}P(x, y)^\beta}\\
    \tilde{x} &= \frac{\sum_{(x, y)\in \mathcal{Z}})P(x, y)^\beta y}{\sum_{(x, y)\in\mathcal{Z}}P(x, y)^\beta}
\end{aligned}
$$

最后更新最优后验估计的协方差，如下所示：

$$
C_{x,y} = \frac{1}{\sum_{x,y}P(x, y)^\beta}\sum_{xy}P(x, y)^\beta(\overrightarrow{t}_{x, y}- \overrightarrow{t}_d)(\overrightarrow{t}_{x, y}- \overrightarrow{t}_d)^T
$$

其中，$\overrightarrow{t}_{x, y}, \overrightarrow{t}_d$ 分别表示该状态和最优状态的运动偏置。

基于 GNSS 定位

作者使用了 RTK 来进行辅助定位，这一部分主要介绍他们怎么对 RTK 结果进行处理来辅助融合，不会关注 RTK 算法本身。RTK 本身依赖于信号强度，在城市场景下（隧道等场景）性能可能会不好，而 Lidar 定位则能够在这种情况下作为补充。这篇论文将 RTK 定位结果和 Lidar 定位结果利用卡尔曼滤波进行松耦合。考虑 RTK 信号容易丢失造成定位结果跳变，这里作者只估计载体的相对位置变化和两个周期之间的时钟漂移。

传感器融合

这一部分将整理如何通过 ESKF 来对 IMU 以及定位观测进行融合。IMU 用来对两个观测（RTK 或者 Lidar）之间的相对运动进行估计。

SINS 运动以及误差方程

SINS 通过对 IMU 测量值积分求出位置、速度以及姿态。在这篇论文里面，作者使用东北天（ENU） 作为导航参考坐标系 n，右前上（RFU）作为载体坐标系 b。同时，考虑地球坐标系 e 以及惯性系 i 的影响。在 n 系下的 的微分方程如下：

$$
\begin{aligned}
    \dot{\boldsymbol{v}} &= \boldsymbol{C}^n_b(\boldsymbol{f}^b-\boldsymbol{b}_a) - (2\omega_{ie}^b + \omega^n_{en})\times\boldsymbol{v}^n + \boldsymbol{g}^n\\
    \dot{\boldsymbol{r}} &= \boldsymbol{R}_c\boldsymbol{v}^n\\
    \dot{\boldsymbol{q}}^n_b &= \frac{1}{2}(\boldsymbol{\omega}^b_{nb}\times)\otimes \boldsymbol{q}^n_b
\end{aligned}
$$

式中，变量含义如下：

• $\boldsymbol{r} = (\lambda, L, a)^T$ 是汽车位置（经度，维度，高度）
• $\boldsymbol{v}^n$ 是汽车速度在导航系下的标识
• $\boldsymbol{q}^n_b, \boldsymbol{C}^n_b$ 是 b 系到 n 系下的姿态四元数和旋转矩阵
• $\boldsymbol{g}^n, \boldsymbol{b}_g, \boldsymbol{b}_a$ 分别是重力，陀螺仪零偏，加速度计零偏
• $\boldsymbol{\omega}^b_{ib}, \boldsymbol{f}^b$ 是 IMU 陀螺仪和加速度值的测量值
• $\boldsymbol{\omega}^\gamma_{\alpha\beta}$ 是 $\beta$ 系相对于 $\alpha$ 系的角速度在 $\gamma$ 系下的表达
• $\boldsymbol{R}_c = \text{diag}(\frac{1}{(R_N + a)\cos{L}}, \frac{1}{(R_N + a)}, 1)$ 能将 IMU 积分结果转换到经纬度以及高度上。

这里涉及到地球系到导航系的转换可能不太直观，可以参考我之前整理的：基于 IMU 的惯性导航解算及误差分析

假设 IMU 的零偏为常值，SINS 的误差模型如下：

$$
\begin{aligned}
    \delta\dot{\boldsymbol{v}}^n &= \boldsymbol{C}^n_b\boldsymbol{f}^b \times \delta\boldsymbol{\psi} - (2\boldsymbol{\omega}^n_{ie} + \boldsymbol{\omega}^n_{en})\times\delta\boldsymbol{v}^n + \boldsymbol{C}^n_b\delta\boldsymbol{f}^b\\
    \delta\dot{\boldsymbol{r}} &= -\boldsymbol{\omega}^n_{en}\times\delta\boldsymbol{r} + \boldsymbol{R}_c\delta\boldsymbol{v}^n\\
    \delta\dot{\psi} &= -\boldsymbol{\omega}^n_{in}\times\delta\boldsymbol{\psi} - \boldsymbol{C}^n_b\delta\boldsymbol{\omega}^b_{ib}
\end{aligned}
$$

滤波状态（预测）方程

接下来进行 ESKF 的预测方程推导：

考虑状态包括 pvq 以及零偏，即 $\boldsymbol{X} = \begin{bmatrix}\boldsymbol{r} & \boldsymbol{v}^n & \boldsymbol{q}^n_b & \boldsymbol{b}_a & \boldsymbol{b}_q\end{bmatrix}^T$，误差状态相应为：$\delta\boldsymbol{X} = \begin{bmatrix}\delta\boldsymbol{r} & \delta\boldsymbol{v}^n & \delta\boldsymbol{q}^n_b & \delta\boldsymbol{b}_a & \delta\boldsymbol{b}_q\end{bmatrix}^T$

ESKF 预测方程为：

$$
\delta\dot{\boldsymbol{X}} = \boldsymbol{F}(\boldsymbol{X})\delta\boldsymbol{X} + \boldsymbol{G}(\boldsymbol{X})\boldsymbol{W}
$$

式中，$\boldsymbol{W} = \begin{bmatrix}\boldsymbol{w}_a & \boldsymbol{w}_g & \boldsymbol{w}_{b_a} & \boldsymbol{w}_{b_g}\end{bmatrix}$ 为系统噪声。$\boldsymbol{F}, \boldsymbol{G}$ 分别是运动 SINS 运动方程对状态以及控制量的雅可比。

滤波观测更新方程

观测部分主要包括 Lidar 以及 GNSS。Lidar 定位模块输出位置以及偏航角，GNSS 仅输出位置，使用标准卡尔曼滤波的更新方程更新即可。

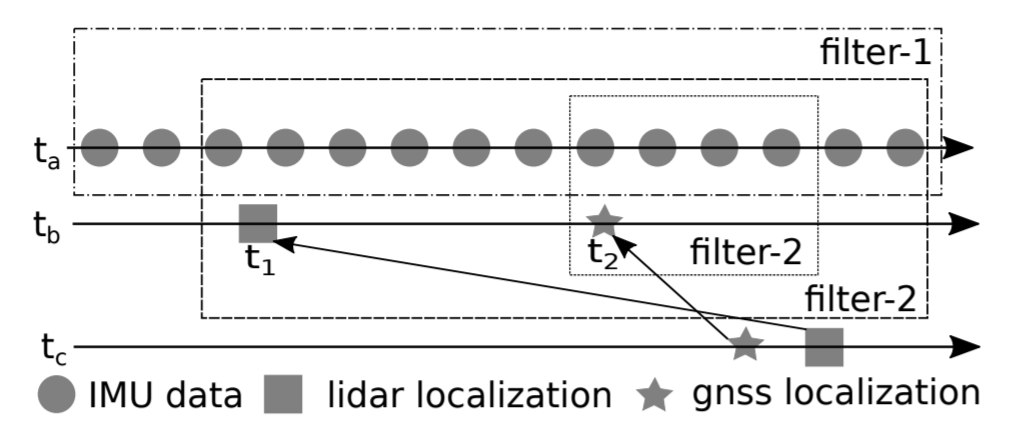
延迟处理

考虑到信号不同步以及测量的延迟问题，作者维护两个滤波以及固定长度的缓存用来保存滤波状态、观测以及 IMU 数据。1 号滤波器在每一个新的 IMU 数据到达时通过积分解算计算实时的 PVA 以及相应的协方差；2 号滤波器用来处理延迟的测量。大概流程如下，每当一个新的测量值在 $t_1$ 时刻到达时：

1. 从缓存器中获取滤波器在 $t_1$ 时刻的状态，并用其更新滤波器 2 的状态
2. 在滤波器 2 中执行 $t_1$ 时刻的观测值更新
3. 在滤波器 2 中使用当前时间之前的 IMU 数据来执行状态预测。如果有另一个观测在 $t_2$ 时刻，则预测至 $t_2$ 时刻就停止。此时，如果 $t_2$ 比 $t_1$ 迟，表明这个观测接收顺序是错误的
4. 如果上一步中有 $t_2$ 时刻的观测，则在 $t_2$ 时刻进行观测更新，然后重复第 3 步
5. 当完成预测和观测且到达当前时刻时，滤波器 1 的状态会从 $t_1$ 更新至当前时间

流程图如下所示：

实验

TODO

结论

TODO