前言
本篇博客主要还是进行不同卡尔曼滤波的数学推导,不会具体涉及到某些传感器。在理解了卡尔曼滤波的数学模型后,对于不同传感器只需要将其测量模型套入运动/观测模型即可。关于基于不同传感器的滤波融合方案,准备之后在阅读论文时再分别整理。
SLAM 中的概率建模
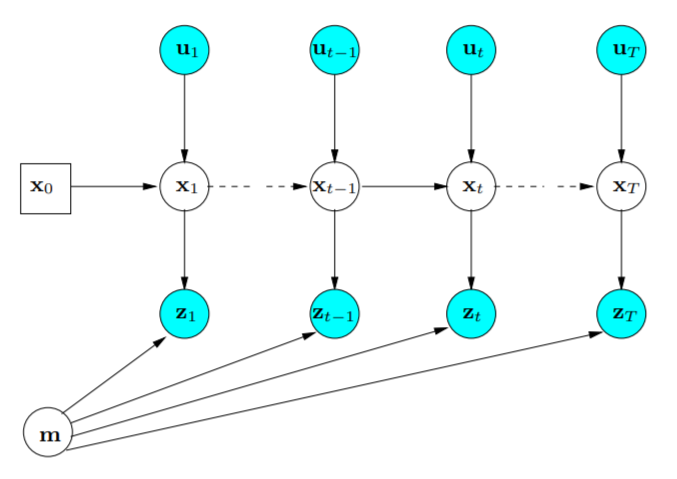
在 SLAM 问题中,我们想要通过滤波方法求解的问题是:求解一个后验概率,即给定一系列观测(和输入)和初始时刻的先验位姿,估计每一个时刻的位姿,如下所示。
$$
p(\boldsymbol{x}_k | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k})
$$
其中,$\boldsymbol{x}_0$ 为先验位姿,$\boldsymbol{u}_{1:k}$ 为 $1:k$ 时刻的输入,$\boldsymbol{z}_{0:k}$ 为 $0:k$ 时刻对环境的观测。我们可以将这些变量通过一个图来表示:
可以看出,在这种图模式下,每个状态仅仅依赖于前一时刻的位姿和输入,和历史位姿无关,这体现了一阶马尔科夫性。同理,观测也只和对应时刻的位姿(以及环境)有关。利用贝叶斯公式对后验概率进行展开有:
$$
\begin{aligned}
p(\boldsymbol{x}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k}) &= \frac{p(\boldsymbol{z}_k | \boldsymbol{x}_k, \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})p(\boldsymbol{x}_k | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})}{p(\boldsymbol{z}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})}
\end{aligned}
$$
由于观测只和位姿有关,因此分母项可以视为一个常数,且分子部分也可以做一部分简化:
$$
\begin{aligned}
p(\boldsymbol{x}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k}) &=\eta p(\boldsymbol{z}_k | \boldsymbol{x}_k, \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})p(\boldsymbol{x}_k | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})\\
&= \eta p(\boldsymbol{z}_k | \boldsymbol{x}_k)p(\boldsymbol{x}_k | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})
\end{aligned}
$$
同时,根据一阶马尔科夫性质可以对当前状态的先验概率进一步化简:
$$
\begin{aligned}
p(\boldsymbol{x}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1}) &= \int p(\boldsymbol{x}_k, \boldsymbol{x}_{k-1} | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})d\boldsymbol{x}_{k-1}\\
&= \int p(\boldsymbol{x}_k| \boldsymbol{x}_{k-1}, \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})p(\boldsymbol{x}_{k-1} | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})d\boldsymbol{x}_{k-1}\\
&= \int p(\boldsymbol{x}_k| \boldsymbol{x}_{k-1}, \boldsymbol{u}_{k})p(\boldsymbol{x}_{k-1} | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})d\boldsymbol{x}_{k-1}
\end{aligned}
$$
因此,结合两部分后验概率可以表示为:
$$
\begin{aligned}
p(\boldsymbol{x}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k}) &= \eta p(\boldsymbol{z}_k | \boldsymbol{x}_k)\int p(\boldsymbol{x}_k| \boldsymbol{x}_{k-1}, \boldsymbol{u}_{k})p(\boldsymbol{x}_{k-1} | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})d\boldsymbol{x}_{k-1}
\end{aligned}
$$
上式即为最基本的贝叶斯滤波公式求解当前状态的后验概率,公式可以分为三部分:
$p(\boldsymbol{z}_k | \boldsymbol{x}_k)$:当前时刻,当前状态下对环境的观测$p(\boldsymbol{x}_k| \boldsymbol{x}_{k-1}, \boldsymbol{u}_{k})$:从前一时刻到当前时刻的状态变化预测$p(\boldsymbol{x}_{k-1} | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})$,上一时刻的状态后验概率
因此,用比较通俗的话来描述一下贝叶斯滤波的过程:
- 首先获得上一时刻状态的后验概率分布
- 对上一时刻所有可能的状态根据运动模型对当前状态进行预测,获得当前状态的先验分布
- 结合当前状态的先验分布和当前观测结果的概率分布计算得到当前状态的后验分布
这个流程中涉及两个部分:怎么从上一时刻的状态量结合输入预测当前时刻状态量;怎么在当前状态下获得对环境的观测分布。这分别对应系统中的两个模型:
运动模型:
$$
\boldsymbol{x}_k = f(\boldsymbol{x}_{k-1}, \boldsymbol{u}_k, \boldsymbol{w}_k)
$$
观测模型:
$$
\boldsymbol{z}_k = f(\boldsymbol{x}_k, m, \boldsymbol{v}_k)
$$
其中,$\boldsymbol{w}_k, \boldsymbol{v}_k$ 分别是运动模型和观测模型的噪声,$m$ 为环境信息。如果问题中不需要对环境信息估计的话,可以不考虑,在大部分视觉 SLAM 中会对环境中的特征点进行优化,此时,特征点会作为环境信息纳入优化中。
此外,在自动控制理论中,运动模型跟输入结合经常表示外界对系统的输入,比如给电机的指令等,有时候会让人混淆运动模型就是主动输入改变系统状态。但实际上,在 SLAM 过程中运动模型和观测模型的区分并不是很明显。比如我们同时有视觉和激光两套 SLAM 系统并且想做松耦合,我们既可以用视觉作为里程计估计前后两帧的位姿变化作为运动模型,然后用激光 SLAM 获得的全局坐标作为系统观测(观测值即为本身的状态)。反过来,我们也可以用激光作为里程计估计前后两帧的的位姿变化,然后用视觉 SLAM 估计出全局的位姿作为观测。
如何求解贝叶斯滤波可以分为两个方向:
- 假设每一时刻的位姿和观测服从高斯分布,应用高斯分布的性质进行求解,为卡尔曼滤波
- 不对位姿和观测的分布作假设,应用蒙特卡洛的思路进行大量模拟,对位姿进行估计,为粒子滤波
卡尔曼滤波 Kalman Filter
原始卡尔曼滤波推导
卡尔曼滤波假设位姿和观测符合高斯分布,且运动模型和观测模型都是线性的,因此运动模型和观测模型可以写成以下形式:
$$
\begin{aligned}
\boldsymbol{x}_k &= \boldsymbol{F}_k\boldsymbol{x}_{k-1} + \boldsymbol{G}_k\boldsymbol{u}_k + \boldsymbol{w}_k, \qquad &\boldsymbol{w} \sim \mathcal{N}(0, \boldsymbol{W})\\
\boldsymbol{z}_k &= \boldsymbol{H}_k\boldsymbol{x}_k + \boldsymbol{v}_k, \qquad &\boldsymbol{v} \sim \mathcal{N}(0, \boldsymbol{V})
\end{aligned}
$$
这里,我们假设运动和观测噪声是直接作用在状态和观测上的,因此,噪声对应的系数矩阵为单位阵。在不同的地方可能会见到不同的假设,比如在噪声上加上不为单位阵的系数矩阵,或者把输入的系数矩阵也作为单位阵。这些假设不会影响推导的思路,只需要按照同样的思路进行些许修改即可。
在下面的推导,为了把状态和先验和后验估计区分开,用 $\check{\boldsymbol{x}}$ 表示先验估计,用 $\hat{\boldsymbol{x}}$ 表示后验估计。其中运动模型中,上一时刻的状态后验写为:
$$
p(\boldsymbol{x}_{k-1}|\boldsymbol{x}_0, \boldsymbol{u}_{1:k-1}, \boldsymbol{z}_{0:k-1}) = \mathcal{N}(\hat{\boldsymbol{x}}_{k-1}, \hat{\boldsymbol{P}}_{k-1})
$$
基于运动模型得到当前时刻的状态位姿的预测值同样服从高斯分布:
$$
\check{\boldsymbol{x}}_k \sim \mathcal{N}(\check{\boldsymbol{\mu}}_k, \check{\boldsymbol{P}}_k)
$$
预测值(先验分布)的均值和协方差矩阵根据运动模型和高斯分布下方差传播的性质得到:
$$
\begin{aligned}
\check{\boldsymbol{\mu}}_k &= \check{\boldsymbol{x}}_k = \boldsymbol{f}(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_k, \boldsymbol{0}) = \boldsymbol{F}_k\boldsymbol{x}_{k-1} + \boldsymbol{G}_k\boldsymbol{u}_k\\
\check{\boldsymbol{P}}_k &= \boldsymbol{F}_{k-1}\hat{\boldsymbol{P}}_{k-1}\boldsymbol{F}_{k-1}^T + \boldsymbol{W}_k
\end{aligned}
$$
显然这一步我们得到的当前时刻的状态值估计的不确定度由于引入了运动误差,相比于上一时刻的不确定度变大了。观测模型的作用就是根据观测估计当前状态的后验概率,降低不确定度。
接下来看后验概率,首先考虑观测和状态的联合分布:
$$
\begin{aligned}
&p(\boldsymbol{x}_k, \boldsymbol{z}_k | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})\\
=& \mathcal{N}
\left(
\begin{bmatrix}
\boldsymbol{\mu}_{x_k}\\
\boldsymbol{\mu}_{z_k}
\end{bmatrix},
\begin{bmatrix}
\boldsymbol{\Sigma}_{x_kx_k} & \boldsymbol{\Sigma}_{x_kz_k}\\
\boldsymbol{\Sigma}_{z_kx_k} & \boldsymbol{\Sigma}_{z_kz_k}\\
\end{bmatrix}
\right)
\end{aligned}
$$
对协方差中的各部分进行推导,会应用到观测模型 $\boldsymbol{z}_k = \boldsymbol{H}\boldsymbol{x}_k + \boldsymbol{v}_k$:
左上角的部分为预测值的协方差
$$
\boldsymbol{\Sigma}_{x_kx_k} = \check{\boldsymbol{P}}_k
$$
右下角的部分计算方法如下所示:
$$
\begin{aligned}
\boldsymbol{\Sigma}_{z_kz_k} &= E\left[(\boldsymbol{z}_k - E[\boldsymbol{z}_k])(\boldsymbol{z}_k - E[\boldsymbol{z}_k]^T\right]\\
&= E\left[(\boldsymbol{H}\boldsymbol{x}_k + \boldsymbol{v}_k - E[\boldsymbol{H}\boldsymbol{x}_k + \boldsymbol{v}_k)(\boldsymbol{H}\boldsymbol{x}_k + \boldsymbol{v}_k - E[\boldsymbol{H}\boldsymbol{x}_k + \boldsymbol{v}_k]^T\right]\\
&= E\left[(\boldsymbol{H}\boldsymbol{x}_k - E[\boldsymbol{H}\boldsymbol{x}_k])(\boldsymbol{H}\boldsymbol{x}_k - E[\boldsymbol{H}\boldsymbol{x}_k]^T\right] + E\left[(\boldsymbol{v}_k - E[\boldsymbol{v}_k])(\boldsymbol{v}_k - E[\boldsymbol{v}_k])^T\right]\\
&= \boldsymbol{H}E\left[(\boldsymbol{x}_k - E[\boldsymbol{x}_k])(\boldsymbol{x}_k - E[\boldsymbol{x}_k]^T\right]\boldsymbol{H}^T + E\left[(\boldsymbol{v}_k - E[\boldsymbol{v}_k])(\boldsymbol{v}_k - E[\boldsymbol{v}_k])^T\right]\\
&= \boldsymbol{H}\check{\boldsymbol{P}}_k\boldsymbol{H}^T + \boldsymbol{V}\\
\end{aligned}
$$
右上角的部分计算方法如下所示:
$$
\begin{aligned}
\boldsymbol{\Sigma}_{x_kz_k} &= E\left[(\boldsymbol{x}_k - E[\boldsymbol{x}_k])(\boldsymbol{z}_k - E[\boldsymbol{z}_k]^T\right]\\
&= E\left[(\boldsymbol{x}_k - \check{\boldsymbol{\mu}}_{x_k})(\boldsymbol{H}\boldsymbol{x}_k - \boldsymbol{H}\check{\boldsymbol{\mu}}_{x_k} + \boldsymbol{v}_k)^T\right]\\
&= E\left[(\boldsymbol{x}_k - \check{\boldsymbol{\mu}}_{x_k})(\boldsymbol{x}_k - \check{\boldsymbol{\mu}}_{x_k})^T\boldsymbol{H}^T\right] + E\left[(\boldsymbol{x}_k - \check{\boldsymbol{\mu}}_{x_k})\boldsymbol{v}_k^T\right]\\
&= \check{\boldsymbol{P}}_k\boldsymbol{H}^T\\
\end{aligned}
$$
左下角可以从右上角的转置获得:
$$
\boldsymbol{\Sigma}_{z_kx_k} = \boldsymbol{\Sigma}_{x_kz_k} = \boldsymbol{H}\check{\boldsymbol{P}}_k^T = \boldsymbol{H}\check{\boldsymbol{P}}_k
$$
参考 SLAM 中的边缘化以及滑动窗口算法 中提到的多元高斯分布的边缘化方法,可以从联合概率获得状态的后验分布:
$$
\begin{aligned}
p(\boldsymbol{x}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k}) &= \mathcal{N}(\hat{\boldsymbol{\mu}}_k, \hat{\boldsymbol{P}}_k)\\
\hat{\boldsymbol{\mu}}_k = \hat{\boldsymbol{x}}_k &= \check{\boldsymbol{x}}_k + (\check{\boldsymbol{P}}_k\boldsymbol{H}^T)(\boldsymbol{H}\check{\boldsymbol{P}}_k\boldsymbol{H}^T + \boldsymbol{V})^{-1}(\boldsymbol{z}_k - \boldsymbol{H}\check{\boldsymbol{x}}_k)\\
\hat{\boldsymbol{P}}_k &= \check{\boldsymbol{P}}_k - (\check{\boldsymbol{P}}_k\boldsymbol{H}^T)(\boldsymbol{H}\check{\boldsymbol{P}}_k\boldsymbol{H}^T + \boldsymbol{V})^{-1}(\boldsymbol{H}\check{\boldsymbol{P}}_k)\\
&= (\boldsymbol{I} - (\check{\boldsymbol{P}}_k\boldsymbol{H}^T)(\boldsymbol{H}\check{\boldsymbol{P}}_k\boldsymbol{H}^T + \boldsymbol{V})^{-1}\boldsymbol{H})\check{\boldsymbol{P}}_k
\end{aligned}
$$
通过这种方式,我们获得当前时刻状态量的后验概率估计,从公式上可以观察到两个现象:
- 利用实际观测值和估计观测值的偏差对当前时刻状态量的估计值进行了一定修正
- 利用观测值的约束降低了当前时刻状态量的不确定度(协方差矩阵)
对上面的推导进行整理,卡尔曼滤波可以分为以下几个阶段:
首先计算当前时刻状态量预测值的均值和方差:
$$
\begin{aligned}
\check{\boldsymbol{\mu}}_k &= \check{\boldsymbol{x}}_k = \boldsymbol{F}_k\boldsymbol{x}_{k-1} + \boldsymbol{G}_k\boldsymbol{u}_k\\
\check{\boldsymbol{P}}_k &= \boldsymbol{F}_{k-1}\hat{\boldsymbol{P}}_{k-1}\boldsymbol{F}_{k-1}^T + \boldsymbol{W}_k
\end{aligned}
$$
然后,计算以下式子,定义为卡尔曼增益:
$$
\boldsymbol{K}_k = (\check{\boldsymbol{P}}_k\boldsymbol{H}^T)(\boldsymbol{H}\check{\boldsymbol{P}}_k\boldsymbol{H}^T + \boldsymbol{V})^{-1}
$$
最后,对预测值使用卡尔曼增益和观测值进行更新:
$$
\begin{aligned}
\hat{\boldsymbol{\mu}}_k = \hat{\boldsymbol{x}}_k &= \check{\boldsymbol{x}}_k + \boldsymbol{K}_k(\boldsymbol{z}_k - \boldsymbol{H}\check{\boldsymbol{x}}_k)\\
\hat{\boldsymbol{P}}_k &= (\boldsymbol{I} - \boldsymbol{K}_k\boldsymbol{H})\check{\boldsymbol{P}}_k
\end{aligned}
$$
原始卡尔曼滤波要求运动模型和观测模型都是线性的,这在实际情况下通常不满足,因此下面几个卡尔曼滤波的变种就是将卡尔曼滤波应用在非线性系统下的几种思路。
扩展卡尔曼滤波 Extended Kalman Filter (EKF)
扩展卡尔曼滤波的思路比较简单。既然卡尔曼滤波只能用在线性系统下,那么只要对非线性系统进行线性化就可以了。因此,对运动模型和观测模型使用泰勒展开进行线性化:
$$
\begin{aligned}
\boldsymbol{x}_k &= f(\boldsymbol{x}_{k-1}, \boldsymbol{u}_k, \boldsymbol{w}_k)\\
&\approx f(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_k, \boldsymbol{0}) + \left.\frac{\partial f}{\partial \boldsymbol{x}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \left.\frac{\partial f}{\partial \boldsymbol{w}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}(\boldsymbol{w}_k - \boldsymbol{0})\\
\boldsymbol{z}_k &= h(\boldsymbol{x}_{k}, \boldsymbol{v}_k)\\
&\approx h(\check{\boldsymbol{x}}_{k}, \boldsymbol{0}) + \left.\frac{\partial h}{\partial\boldsymbol{x}}\right|_{\check{\boldsymbol{x}}_{k}, \boldsymbol{0}}(\boldsymbol{x}_{k} - \check{\boldsymbol{x}}_{k}) + \left.\frac{\partial h}{\partial\boldsymbol{v}}\right|_{\check{\boldsymbol{x}}_k, \boldsymbol{0}}(\boldsymbol{v}_k - \boldsymbol{0})
\end{aligned}
$$
将上式中四个雅可比分别用四个矩阵表示:
$$
\begin{aligned}
\boldsymbol{F}_k &= \left.\frac{\partial f}{\partial \boldsymbol{x}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}\\
\boldsymbol{Q}_k &= \left.\frac{\partial f}{\partial \boldsymbol{w}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}\\
\boldsymbol{H}_k &= \left.\frac{\partial h}{\partial\boldsymbol{x}}\right|_{\check{\boldsymbol{x}}_{k}, \boldsymbol{0}}\\
\boldsymbol{R}_k &= \left.\frac{\partial h}{\partial\boldsymbol{v}}\right|_{\check{\boldsymbol{x}}_k, \boldsymbol{0}}
\end{aligned}
$$
因此,线性化式子可以写成:
$$
\begin{aligned}
\boldsymbol{x}_k &\approx \check{\boldsymbol{x}}_{k} + \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \boldsymbol{Q}_k\boldsymbol{w}_k\\
\boldsymbol{z}_k &\approx \check{\boldsymbol{z}}_k + \boldsymbol{H}_k(\boldsymbol{x}_{k} - \check{\boldsymbol{x}}_{k}) + \boldsymbol{R}_k\boldsymbol{v}_k
\end{aligned}
$$
接下来为了求卡尔曼增益,我们需要求线性化后的运动模型和观测模型的均值和协方差:
运动模型:
$$
\begin{aligned}
E[\boldsymbol{x}_k] &= \check{\boldsymbol{\mu}}_k = E[\check{\boldsymbol{x}}_{k} + \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \boldsymbol{Q}_k\boldsymbol{w}_k]\\
&= \check{\boldsymbol{x}}_{k} + \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \hat{\boldsymbol{x}}_{k-1})\\
E[(\boldsymbol{x}_k - E[\boldsymbol{x}_k])(\boldsymbol{x}_k - E[\boldsymbol{x}_k])^T] &= \check{\boldsymbol{P}}_k \approx E[\boldsymbol{Q}_k\boldsymbol{w}_k\boldsymbol{w}_k^T\boldsymbol{Q}_{k}^T]\\
&= \boldsymbol{Q}_k\boldsymbol{W}\boldsymbol{Q}^T
\end{aligned}
$$
同理可得观测模型:
$$
\begin{aligned}
E(\boldsymbol{z}_k) &\approx \check{\boldsymbol{z}}_k + \boldsymbol{H}_k(\boldsymbol{x}_k - \check{\boldsymbol{x}}_k)\\
E((\boldsymbol{z}_k - E(\boldsymbol{z}_k))(\boldsymbol{z}_k - E(\boldsymbol{z}_k))^T) &\approx E[\boldsymbol{R}\boldsymbol{v}_k\boldsymbol{v}_k^T\boldsymbol{R}^T] = \boldsymbol{R}\boldsymbol{V}\boldsymbol{R}^T
\end{aligned}
$$
这样我们得到了线性化后的运动和观测模型的概率分布,后续只需要将均值和协方差代入经典卡尔曼滤波公式中即可。
迭代扩展卡尔曼滤波 Iterative Extended Kalman Filter (IEKF)
IEKF 是在 EKF 上考虑了线性化误差的问题,EKF 的线性化点选择了在当前时刻的先验估计 $\check{\boldsymbol{x}}_k$ 进行。过程中线性化误差的会随着线性化点和工作点和差距而别大。因此一个很直观的想法是当我们通过这个线性化点得到当前时刻的后验估计 $\hat{\boldsymbol{x}}_k$ ,我们能不能以这个作为线性化点重新对观测模型进行线性化并重新估计当前时刻状态的后验分布。这个就是 IEKF 的思想。
大致上的流程就是先进行一次 EKF,得到第一次后验估计重复进行以下步骤:
$$
\begin{aligned}
\boldsymbol{x}_{op, k} &= \hat{\boldsymbol{x}}_k\\
\boldsymbol{z}_k &\approx \boldsymbol{z}_{op, k} + \boldsymbol{H}_{op, k}(\boldsymbol{x}_{k} - \boldsymbol{x}_{op, k}) + \boldsymbol{R}_k\boldsymbol{v}_k\\
\boldsymbol{K}_k &= (\check{\boldsymbol{P}}_k\boldsymbol{H}_{op, k}^T)(\boldsymbol{H}_{op, k}\check{\boldsymbol{P}}_k\boldsymbol{H}_{op, k}^T + \boldsymbol{R}\boldsymbol{V}\boldsymbol{R}^T)^{-1}\\
\hat{\boldsymbol{\mu}}_k = \hat{\boldsymbol{x}}_k &= \check{\boldsymbol{x}}_k + \boldsymbol{K}_k(\boldsymbol{z}_k - \boldsymbol{H}_{op, k}(\check{\boldsymbol{x}}_k-\boldsymbol{x}_{op,k}))\\
\hat{\boldsymbol{P}}_k &= (\boldsymbol{I} - \boldsymbol{K}_k\boldsymbol{H}_{op, k})\check{\boldsymbol{P}}_k
\end{aligned}
$$
基于误差状态的卡尔曼滤波 Error State Extended Kalman Filter (ES-EKF)
ES-EKF 将载体的真实状态分为:名义状态(Nomimal State, 不考虑任何误差得出的理想状态)和误差状态(Error State, 名义状态和真实状态的差值),如下所示:
$$
\boldsymbol{x} = \check{\boldsymbol{x}} + \delta\boldsymbol{x}
$$
EK-EKF 的思想就是不对真实状态进行滤波,而改为对误差状态滤波。基本流程是:对名义状态使用不含误差的运动模型一直进行更新,对误差状态进行滤波(包括预测和更新),并将其添加至名义状态中对其进行修正,使其更接近真实值。如下所示:
对运动模型进行线性化,线性化点在上一时刻的名义状态(和上一时刻的状态先验估计一样)处:
$$
\begin{aligned}
\boldsymbol{x}_k &= f(\boldsymbol{x}_{k-1}, \boldsymbol{u}_k, \boldsymbol{w}_k)\\
&\approx f(\check{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_k, \boldsymbol{0}) + \left.\frac{\partial f}{\partial \boldsymbol{x}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}(\boldsymbol{x}_{k-1} - \check{\boldsymbol{x}}_{k-1}) + \left.\frac{\partial f}{\partial \boldsymbol{w}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}(\boldsymbol{w}_k - \boldsymbol{0})\\
&= \check{\boldsymbol{x}}_{k} + \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \check{\boldsymbol{x}}_{k-1}) + \boldsymbol{Q}_{k}\boldsymbol{w}_k \\
\end{aligned}
$$
移一下项可以得到关于误差状态的线性运动模型:
$$
\begin{aligned}
\boldsymbol{x}_k - \check{\boldsymbol{x}}_{k} &= \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \check{\boldsymbol{x}}_{k-1}) + \boldsymbol{Q}_{k}\boldsymbol{w}_{k}\\
\Rightarrow\delta\boldsymbol{x}_k &= \boldsymbol{F}_{k-1}\delta\boldsymbol{x}_{k-1} + \boldsymbol{Q}_{k}\boldsymbol{w}_{k}
\end{aligned}
$$
对观测模型也可以做类似处理:
$$
\begin{aligned}
\boldsymbol{z}_k &= h(\boldsymbol{x}_{k}, \boldsymbol{v}_k)\\
&\approx h(\check{\boldsymbol{x}}_{k}, \boldsymbol{0}) + \left.\frac{\partial h}{\partial\boldsymbol{x}}\right|_{\check{\boldsymbol{x}}_{k}, \boldsymbol{0}}(\boldsymbol{x}_{k} - \check{\boldsymbol{x}}_{k}) + \left.\frac{\partial h}{\partial\boldsymbol{v}}\right|_{\check{\boldsymbol{x}}_k, \boldsymbol{0}}(\boldsymbol{v}_k - \boldsymbol{0})\\
&= h(\check{\boldsymbol{x}}_{k}, \boldsymbol{0}) + \boldsymbol{H}_{k}(\boldsymbol{x}_{k} - \check{\boldsymbol{x}}_{k}) + \boldsymbol{R}_k\boldsymbol{v}_k\\
&= h(\check{\boldsymbol{x}}_{k}, \boldsymbol{0}) + \boldsymbol{H}_{k}\delta\boldsymbol{x}_k + \boldsymbol{R}_k\boldsymbol{v}_k\\
\end{aligned}
$$
预测和更新处理和原始卡尔曼滤波基本一致:
预测阶段,预测当前时刻的名义状态(如果上一时刻没有观测更新,则可以用上一时刻的先验,否则用后验估计),同样包括均值和方差:
$$
\begin{aligned}
\check{\boldsymbol{\mu}}_k &= \check{\boldsymbol{x}}_k = f(\boldsymbol{x}_{k-1}, \boldsymbol{u}_k, \boldsymbol{0})\\
\check{\boldsymbol{P}}_k &= \boldsymbol{F}_{k-1}\boldsymbol{P}_{k-1}\boldsymbol{F}_{k-1}^T + \boldsymbol{Q}_k\boldsymbol{W}\boldsymbol{Q}^T
\end{aligned}
$$
当有新的观测进来时,使用观测对误差状态进行一次更新(这里是和原始卡尔曼滤波不一样的地方):
计算卡尔曼增益和更新后的误差状态:
$$
\begin{aligned}
\boldsymbol{K}_k &= \check{\boldsymbol{P}}_{k}\boldsymbol{H}_k^T(\boldsymbol{H}_k\check{\boldsymbol{P}}_k\boldsymbol{H}_k^T + \boldsymbol{R})^{-1}\\
\delta\boldsymbol{x}_k &= \boldsymbol{K}_k(\boldsymbol{z}_k - h(\check{\boldsymbol{x}}_k, \boldsymbol{0}))\\
\end{aligned}
$$
然后用更新后的误差状态更新真实状态作为后验估计:
$$
\begin{aligned}
\hat{\boldsymbol{\mu}}_x = \hat{\boldsymbol{x}}_k &= \check{\boldsymbol{x}}_k + \delta\boldsymbol{x}_k\\
\hat{\boldsymbol{P}}_k &= (\boldsymbol{I} - \boldsymbol{K}_k\boldsymbol{H}_k)\check{\boldsymbol{P}}_k
\end{aligned}
$$
用误差状态作为估计状态量有这么几个好处:
- 旋转的误差状态可以避免过参数化的问题,比较好操作。假如我们用四元数作为估计状态量,那么实际上它只有三个自由度,因此在更新的时候需要做一点特殊处理。如果使用误差状态则没有这个问题
- 误差状态通常比较小,可以有效控制线性化误差
- 误差状态通常变化比较缓慢,因此更新频率的容忍度较高,可以以较慢的频率更新
如果本身系统就是线性化的那么不需要线性化环节,为 ESKF。上述流程基本不变,只需要自己推导一下误差更新方程即可。IMU 的误差更新方程推导可以参考:基于 IMU 的惯性导航解算及误差分析
无迹卡尔曼滤波 Unscented Kalman Filter (UKF)
UKF 的思想是按照高斯分布的性质进行采样选出若干个 sigma 点,用这些点来模拟当前的先验分布,对这些点通过运动和观测模型进行非线性转换。再分析转换后的点的分布近似当前时刻的后验分布。具体过程如下:
- 预测步骤:
先将噪声和上一时刻的后验状态组合成一个新状态,用新的均值和方差表示:
$$
\begin{aligned}
\boldsymbol{\mu}_y &= \begin{bmatrix}
\hat{\boldsymbol{x}}_{k-1}\\
\boldsymbol{0}
\end{bmatrix}\\
\boldsymbol{\Sigma}_{yy} &= \begin{bmatrix}
\hat{\boldsymbol{P}}_{k-1}& \boldsymbol{0}\\
0 & \boldsymbol{W}_k
\end{bmatrix}
\end{aligned}
$$
然后,我们通过以下方法选出 $2L + 1$ 个 sigma 点用来对当前的分布进行近似。
$$
\begin{aligned}
\boldsymbol{LL}^T &= \boldsymbol{\Sigma}_{yy}\\
\boldsymbol{y}_0 &= \boldsymbol{\mu}_y\\
\boldsymbol{y}_i &= \boldsymbol{\mu}_y + \sqrt{L + \kappa}\text{col}_i\boldsymbol{L}, &\qquad i = 1, 2, ..., L\\
\boldsymbol{y}_{i+L} &= \boldsymbol{\mu}_y - \sqrt{L + \kappa}\text{col}_i\boldsymbol{L}, &\qquad i = 1, 2, ..., L
\end{aligned}
$$
将得到的 Sigma 点重新分解成状态和噪声的形式:
$$
\boldsymbol{y}_i = \begin{bmatrix}
\hat{\boldsymbol{x}}_{k-1, i}\\
\boldsymbol{w}_{k, i}
\end{bmatrix}
$$
将每个 Sigma 点传入运动模型中:
$$
\check{\boldsymbol{x}}_{k, i} = f(\hat{\boldsymbol{x}}_{k-1, i}, \boldsymbol{u}_k, \boldsymbol{w}_{k, i}) \qquad i = 0, 1, ..., 2L
$$
此时,我们获得了当前时刻状态量先验分布的 sigma 点,按照一定权重组合起来,每个 Sigma 点的权重满足以下条件:
$$
\alpha_i = \left\{
\begin{aligned}
&\frac{\kappa}{L+\kappa}, &\qquad i = 0\\
&\frac{1}{2}\frac{1}{L + \kappa}&\qquad\text{others}
\end{aligned}
\right.
$$
将这些点按照权重组合得到当前时刻预测状态的均值和方差:
$$
\begin{aligned}
\check{\boldsymbol{x}}_k &= \check{\boldsymbol{\mu}}_x = \sum_{i = 0}^{2L}\alpha_{i}\check{\boldsymbol{x}}_{k, i}\\
\check{\boldsymbol{P}}_k &= \boldsymbol{\Sigma}_{xx} = \sum_{i = 0}^{2L}\alpha_i(\check{\boldsymbol{x}}_{k, i}-\check{\boldsymbol{\mu}}_x)(\check{\boldsymbol{x}}_{k, i}-\check{\boldsymbol{\mu}}_x)^T
\end{aligned}
$$
- 校正步骤:
思路类似,首先将当前时刻先验估计和观测噪声组合起来:
$$
\begin{aligned}
\boldsymbol{\mu}_y &= \begin{bmatrix}
\check{\boldsymbol{x}}_{k}\\
\boldsymbol{0}
\end{bmatrix}\\
\boldsymbol{\Sigma}_{yy} &= \begin{bmatrix}
\check{\boldsymbol{P}}_{k}& \boldsymbol{0}\\
0 & \boldsymbol{V}_k
\end{bmatrix}
\end{aligned}
$$
然后,我们通过以下方法选出 $2L + 1$ 个 sigma 点用来对当前的先验分布进行近似。
$$
\begin{aligned}
\boldsymbol{LL}^T &= \boldsymbol{\Sigma}_{yy}\\
\boldsymbol{y}_0 &= \boldsymbol{\mu}_y\\
\boldsymbol{y}_i &= \boldsymbol{\mu}_y + \sqrt{L + \kappa}\text{col}_i\boldsymbol{L}, &\qquad i = 1, 2, ..., L\\
\boldsymbol{y}_{i+L} &= \boldsymbol{\mu}_y - \sqrt{L + \kappa}\text{col}_i\boldsymbol{L}, &\qquad i = 1, 2, ..., L
\end{aligned}
$$
接下来同样将 sigma 点展开成状态和观测噪声:
$$
\boldsymbol{y}_i = \begin{bmatrix}
\check{\boldsymbol{x}}_{k, i}\\
\boldsymbol{v}_{k, i}
\end{bmatrix}
$$
将每个 sigma 的状态和噪声传入观测模型:
$$
\check{\boldsymbol{z}}_{k, i} = h(\check{\boldsymbol{x}}_{k, i}, \boldsymbol{v}_{k, i}) \qquad i = 0, 1, ..., 2L
$$
按照一定权重(和预测步骤一样),计算卡尔曼增益和校正步骤需要的参数:
$$
\begin{aligned}
\boldsymbol{\mu}_{z, k} &= \sum_{i = 0}^{2L}\alpha_{i}\check{\boldsymbol{z}}_{k, i}\\
\boldsymbol{\Sigma}_{zz, k} &= \sum_{i = 0}^{2L}\alpha_i(\check{\boldsymbol{z}}_{k, i}-\boldsymbol{\mu}_{z, k})(\check{\boldsymbol{z}}_{k, i}-\boldsymbol{\mu}_{z, k})^T\\
\boldsymbol{\Sigma}_{xz, k} &= \sum_{i = 0}^{2L}\alpha_i(\check{\boldsymbol{x}}_{k, i}-\check{\boldsymbol{x}}_{k})(\check{\boldsymbol{z}}_{k, i}-\boldsymbol{\mu}_{z, k})^T
\end{aligned}
$$
有了这几个参数,可以计算出卡尔曼增益并应用校正方程对先验估计的均值和方差进行更新。
粒子滤波 Particle Filter (PF)
粒子滤波的思想和 UKF 有点类似,不过它不假设状态和噪声为高斯分布,因此没办法按照规律选择采样点,所以粒子滤波的思想是直接根据大数定律进行很多次采样,用这些采样点来做非线性变换,并且对结果重新进行计算概率密度。
具体步骤如下:
从上一时刻的后验分布和噪声的联合分布中,抽取 M 个样本(粒子):
$$
\begin{bmatrix}
\hat{\boldsymbol{x}}_{k-1, m}\\
\boldsymbol{w}_{k, m}
\end{bmatrix}\leftarrow
p(\boldsymbol{x}_{k-1}|\boldsymbol{0}_0, \boldsymbol{u}_{1:k-1}, \boldsymbol{z}_{1:k-1})p(\boldsymbol{w})
$$
将每个例子通过运动模型进行非线性变换:
$$
\check{\boldsymbol{x}}_{k, m} = f(\hat{\boldsymbol{x}}_{k-1, m}, \boldsymbol{u}_k, \boldsymbol{w}_{k, m})
$$
用这些粒子来近似当前时刻先验状态分布。此时我们不知道哪个粒子更接近真实值,观测的作用就是对各个粒子的正确性进行判断,从而分配权重,方法如下所示:
每个粒子的权重表示在该粒子下出现当前观测的可能性:
$$
\alpha_{k, m} = \eta p(\boldsymbol{z}_k | \check{\boldsymbol{x}}_{k, m})
$$
用观测模型得到在当前各个粒子状态下的理论观测分布:
$$
\check{\boldsymbol{z}}_{k, m} = h(\check{\boldsymbol{x}}_{k, m}, \boldsymbol{0})
$$
计算在该分布下,实际观测的概率:$p(\boldsymbol{z}_k | \check{\boldsymbol{z}}_{k, m})$
对所有粒子计算这个概率,并进行归一化获得权重。去掉权重较小的粒子,对剩余的粒子按照其权重进行重采样。