VINS-Mono 大致算法流程

系统总览

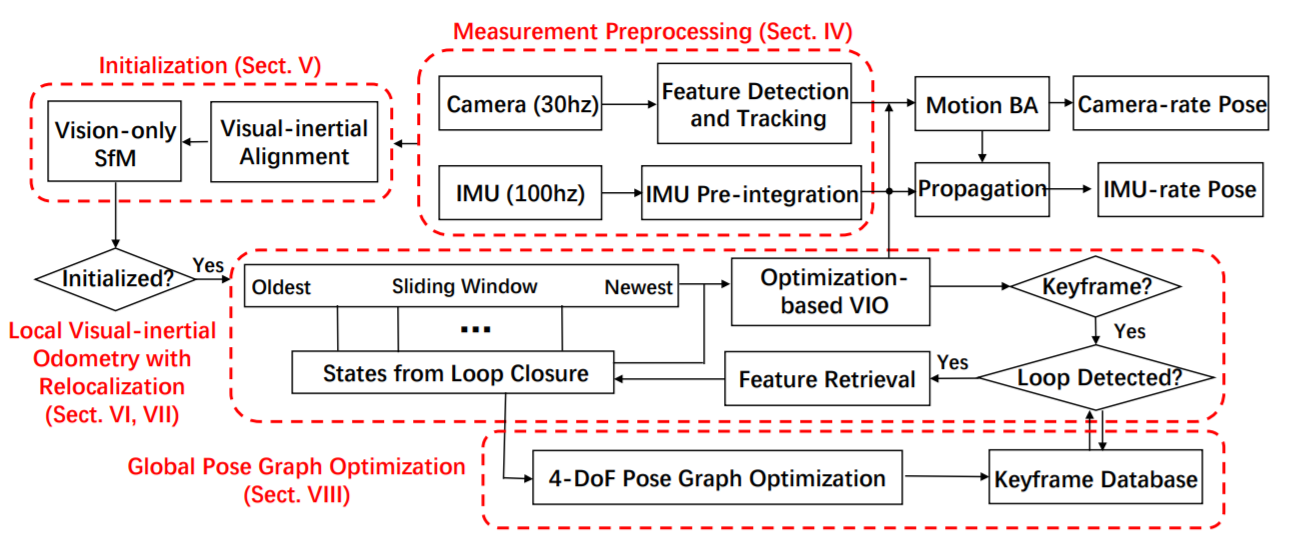
VINS-MONO 大致可以分为 3 个部分：系统初始化、数据处理、滑动窗口局部位姿优化、回环检测以及全局优化。

如下图所示：

其中：系统初始化负责估计 IMU 和相机之间的外参，估计传感器的偏置以及初始速度以及将 IMU 轨迹和视觉姿态对齐等等；数据处理部分负责从视觉信息中提取并追踪特征、以及进行 IMU 预积分；滑动窗口局部位姿估计顾名思义负责在一个滑动窗口内进行位姿优化；回环检测部分检测是否有回环以及按需进行全局优化。

系统初始化

VINS-MONO 中系统初始化流程包括以下几步：

估计 IMU 和相机之间的旋转外参
估计 IMU 陀螺仪的偏置
估计重力方向，初速度以及尺度因子
求解世界坐标系和初始相机坐标系之间的旋转以及轨迹对齐

滑动窗口 SfM 获得初始化所需数据

VINS-MONO 中一共涉及三个坐标系相互转换，包括：世界坐标系 $w$ 、任意时刻的相机坐标系 $c$ 、任意时刻的载体（IMU）坐标系 $b$ 。其中，由于没有 GPS 等绝对测量传感器，因此这里先考虑使用初始时刻的相机坐标系 $c_0$ 作为世界坐标系，然后进行一个小规模的位姿估计（特征提取追踪、五点法估计位姿、三角化恢复特征点坐标、全局 BA 最小化重投影误差）得到一系列 $\bar{\boldsymbol{p}}_{c_0c_k}, \boldsymbol{R}_{c_0c_k}(\boldsymbol{q}_{c_0c_k})$ ，由于单目相机没办法估计绝对尺度，因此这里得到平移信息的尺度是不确定的。

此外，我们忽略在载体运行过程的震荡，假设 IMU 和相机之间的外参不变，假设我们粗略知道外参 $\boldsymbol{T}_{bc}$ （如果对旋转外参不确定可以参考下一部分），我们可以得到以下位姿约束关系：

$$
\begin{aligned}
    \boldsymbol{R}_{c_0b_k} &= \boldsymbol{R}_{c_0c_k}\boldsymbol{R}_{bc}^{-1}\\
    s\bar{\boldsymbol{p}}_{c_0b_k} &= s\bar{\boldsymbol{p}}_{c_0c_k} - \boldsymbol{R}_{c_0b_k}\boldsymbol{p}_{bc}
\end{aligned}
$$

上式中，由于在单目相机位姿估计没有办法确定尺度信息，所以这里使用 $\bar{\boldsymbol{t}}$ 表示非米制单位的平移， $s$ 为尺度因子，可以将非米制单位的平移转换为米制。第二条式子中描述了 IMU 在世界坐标系下的位姿、相机在坐标系下的位姿以及世界坐标系下IMU 和相机的之间的外参的关系。上式也可以写作：

$$
\begin{aligned}
    \bar{\boldsymbol{p}}_{c_0b_k} &= \bar{\boldsymbol{p}}_{c_0c_k} - \frac{1}{s}\boldsymbol{R}_{c_0b_k}\boldsymbol{p}_{bc}\\
    \bar{\boldsymbol{p}}_{c_0c_k} &= \frac{1}{s}\boldsymbol{R}_{c_0b_k}\boldsymbol{p}_{bc} + \bar{\boldsymbol{p}}_{c_0b_k}
\end{aligned}
$$

在后续的处理中，我们会将世界坐标系与重力方向对齐（使用 ENU 坐标系），因此世界坐标系和初始时刻相机坐标系之间实际上存在一个旋转关系。

旋转外参估计

如果我们对旋转外参不确定，我们可以先对旋转外参进行估计，相邻两时刻 $k, k+1$ 之间，对于 IMU 可以计算出旋转预积分： $\boldsymbol{q}_{b_kb_{k+1}}$ ，对于视觉测量可以通过第一部分估计出的： $\boldsymbol{q}_{c_kc_{k+1}}$ 。则对于旋转部分外参有：

$$
\boldsymbol{q}_{b_kb_{k+1}}\otimes\boldsymbol{q}_{bc} = \boldsymbol{q}_{bc} \otimes \boldsymbol{q}_{c_kc_{k+1}}
$$

利用四元数运算的性质，有：

$$
\begin{aligned}
    \boldsymbol{q}_{b_kb_{k+1}}\otimes\boldsymbol{q}_{bc} &= [\boldsymbol{q}_{b_kb_{k+1}}]_L\boldsymbol{q}_{bc}\\
    \boldsymbol{q}_{bc} \otimes \boldsymbol{q}_{c_kc_{k+1}} &= [\boldsymbol{q}_{c_kc_{k+1}}]_R\boldsymbol{q}_{bc}\\
    \Rightarrow([\boldsymbol{q}_{b_kb_{k+1}}]_L - [\boldsymbol{q}_{c_kc_{k+1}}]_R)\boldsymbol{q}_{bc} &= \boldsymbol{0}
\end{aligned}
$$

设 $\boldsymbol{Q}^{k}_{k+1} = [\boldsymbol{q}_{b_kb_{k+1}}]_L - [\boldsymbol{q}_{c_kc_{k+1}}]_R$ ，有 $\boldsymbol{Q}^k_{k+1}\boldsymbol{q}_{bc}=\boldsymbol{0}$ , 因此，通过旋转之间的约束，利用多个时间段的测量数据，我们可以构建出一个关于旋转外参的线性方程组。但对于不同时段的测量，我们应该根据其角度误差分配合适的权重，角度误差的计算方式为通过两个测量角度计算 $\boldsymbol{R}_{b_kc_{k+1}}$ ，然后对这两个结果相减，如果旋转外参准确的话，结果应该接近 0。具体而言则是，计算 $(\boldsymbol{R}_{b_kb_{k+1}}\hat{\boldsymbol{R}}_{bc})^{-1}(\hat{\boldsymbol{R}}_{bc}\boldsymbol{R}_{c_kc_{k+1}})$ ，利用旋转矩阵和轴角的性质 $\text{tr}(\boldsymbol{R}) = 1+ 2\cos{\theta}$ ，定义旋转矩阵的角度误差为：

$$
\begin{aligned}
r^k_{k+1} &= \arccos{((\text{tr}((\boldsymbol{R}_{b_kb_{k+1}}\hat{\boldsymbol{R}}_{bc})^{-1}(\hat{\boldsymbol{R}}_{bc}\boldsymbol{R}_{c_kc_{k+1}}))-1)/2)}\\
&= \arccos{((\text{tr}(\hat{\boldsymbol{R}}_{bc}^{-1}\boldsymbol{R}_{b_kb_{k+1}}^{-1}\hat{\boldsymbol{R}}_{bc}\boldsymbol{R}_{c_kc_{k+1}})-1)/2)}
\end{aligned}
$$

根据这个角度误差，VINS-MONO 的权重分配策略如下：

$$
w^k_{k+1} = \left\{
\begin{aligned}
    &1, \quad &r^k_{k+1} < \text{threshold}\\
    &\frac{\text{threshold}}{r^k_{k+1}}, \quad& \text{otherwise}
\end{aligned}
\right.
$$

因此，计算并记录多段 IMU 的观测值（计算预积分）和相机位姿估计，可以构建线性方程组如下：

$$
\begin{bmatrix}
    w_1^0\boldsymbol{Q}^0_1\\
    w_2^1\boldsymbol{Q}^1_2\\
    ...\\
    w^{N-1}_N\boldsymbol{Q}^{N-1}_N
\end{bmatrix}\boldsymbol{q}_{bc} = \boldsymbol{Q}_{N}\boldsymbol{q}_{bc} = \boldsymbol{0}
$$

上式中，我们对每一个时间的测量值根据其角度误差分配一个鲁棒核权重用于进行权重的调节，VINS-MONO 中使用 SVD 分解进行求解。

至于平移外参，相对于旋转部分来说对系统精度的影响不会太大，并且尺度相对而言也不是很大。所以可以暂时在初始化过程中粗略设定为一个值在后续的过程中对其再进行优化。

陀螺仪 Bias 估计

利用旋转约束，可以对陀螺仪的偏置进行估计，思路和上一部分类似，计算相机的姿态和 IMU 的姿态并利用外参联系起来，得到： $\boldsymbol{q}_{c_0b_{k+1}}^{-1}\otimes\boldsymbol{q}_{c_0b_k}\otimes\boldsymbol{\gamma}_{b_kb_{k+1}}$ ，理论上这个量应该等于 $(0, 0, 0, 1)$ 即没有旋转，但由于估计精度的问题以及零偏的问题会使其不为 0，因此我们要找出一个零偏 $\boldsymbol{b}^g$ 使得这个量的 xyz 部分最小化，即求解以下问题：

$$
\begin{aligned}
    &\arg\min_{\delta\boldsymbol{b}^g}\sum_{k\in B}||2\left[\boldsymbol{q}_{c_0b_{k+1}}^{-1}\otimes\boldsymbol{q}_{c_0b_k}\otimes\boldsymbol{\gamma}_{b_kb_{k+1}}\right]_{xyz}||^2\\
    &\boldsymbol{\gamma}_{b_kb_{k+1}}\approx\tilde{\boldsymbol{\gamma}}_{b_kb_{k+1}}\otimes\begin{bmatrix}
        1\\\frac{1}{2}\boldsymbol{J}^{\boldsymbol{q}}_{b^g}\delta\boldsymbol{b}^g
    \end{bmatrix}
\end{aligned}
$$

上述问题是一个最小二乘问题，可以通过求残差对优化变量的雅可比矩阵 $\boldsymbol{J} = \frac{\partial\boldsymbol{r}}{\partial\boldsymbol{x}}$ ，构建信息矩阵 $\boldsymbol{H} = \boldsymbol{J}^T\boldsymbol{J}$ 和信息向量 $\boldsymbol{b} = -\boldsymbol{J}\boldsymbol{r}$ ，最后求解线性方程组 $\boldsymbol{Hx} = \boldsymbol{b}$ 即可。

至于加速度计的偏置，由于其偏置和重力加速度的大小小若干个数量级，所以这里不做特别估计。具体推导证明可以参考：Robust initialization of monocular visual-inertial estimation on aerial robots

初始化速度、重力和尺度因子估计

在这一部分中，我们需要估计以下变量：

$\boldsymbol{v}^{b_0}_0, \boldsymbol{v}^{b_1}_1, ..., \boldsymbol{v}^{b_n}_n$ ： $k$ 时刻下（与时间关键帧时间重合），载体坐标系（b 系）相对于参考惯性系（这里是世界坐标系）下的速度在载体下的表示
$\boldsymbol{g}^{c_0}$ ：重力在初始时刻相机坐标系下的坐标表示，用于计算初始相机坐标系相对于世界坐标系的姿态
$s$ ：单目相机位姿估计中的尺度因子，可以将估计的非米制位置转换为米制单位

首先，基于 IMU 的预积分，我们可以得到任意两帧之间的预积分量的观测方程，如下所示：

$$
\begin{bmatrix}
    \tilde{\boldsymbol{\alpha}}_{{b_k}b_{k+1}}\\
    \tilde{\boldsymbol{\beta}}_{{b_k}b_{k+1}}\\
    \tilde{\boldsymbol{\gamma}}_{{b_k}b_{k+1}}\\
    \boldsymbol{0}\\
    \boldsymbol{0}\\
\end{bmatrix} = 
\begin{bmatrix}
    \boldsymbol{R}_{b_kw}(\boldsymbol{p}_{wb_{k+1}} - \boldsymbol{p}_{wb_{k}} + \frac{1}{2}\boldsymbol{g}^w\Delta t^2 - \boldsymbol{v}^w_{b_k}\Delta t)\\
    \boldsymbol{R}_{b_kw}(\boldsymbol{v}^w_{b_{k+1}} + \boldsymbol{g}^w\Delta t - \boldsymbol{v}^w_{b_k})\\
    \boldsymbol{q}_{wb_{k}}^{-1}\otimes\boldsymbol{q}_{wb_{k+1}}\\
    \boldsymbol{b}^a_{b_{k+1}} - \boldsymbol{b}^a_{b_{k}}\\
    \boldsymbol{b}^g_{b_{k+1}} - \boldsymbol{b}^g_{b_{k}}\\
\end{bmatrix}
$$

接下来可以通过观测模型构建状态量的约束进行速度估计。首先将 $c_0$ 视为世界坐标系，将状态值代入 $\boldsymbol{\alpha}_{b_kb_{k+1}}, \boldsymbol{\beta}_{b_kb_{k+1}}$ 有：

$$
\begin{aligned}
    \boldsymbol{\alpha}_{b_kb_{k+1}} &= \boldsymbol{R}_{b_kc_0}(s\bar{\boldsymbol{p}}_{c_0b_{k+1}} - s\bar{\boldsymbol{p}}_{c_0b_{k}} + \frac{1}{2}\boldsymbol{g}^{c_0}\Delta t^2 - \boldsymbol{R}_{c_0b_k}\boldsymbol{v}^{b_k}_{b_k}\Delta t)\\
    \boldsymbol{\beta}_{{b_k}b_{k+1}}&= \boldsymbol{R}_{b_kc_0}(\boldsymbol{R}_{c_0b_{k+1}}\boldsymbol{v}^{b_{k+1}}_{b_{k+1}} + \boldsymbol{g}^{c_0}\Delta t - \boldsymbol{R}_{c_0b_k}\boldsymbol{v}^{b_k}_{b_k})
\end{aligned}
$$

上式中， $\bar{\boldsymbol{p}}_{c_0b_{k+1}}, \bar{\boldsymbol{p}}_{c_0b_{k}}$ 并没有计算出来，但是我们知道它和 $\bar{\boldsymbol{p}}_{c_0c_{k+1}}, \boldsymbol{T}_{bc}$ 之间的几何约束关系，因此代入得：

$$
\begin{aligned}
s\bar{\boldsymbol{p}}_{c_0b_k} &= s\bar{\boldsymbol{p}}_{c_0c_k} - \boldsymbol{R}_{c_0b_k}\boldsymbol{p}_{bc}\\
\Rightarrow s\bar{\boldsymbol{p}}_{c_0b_{k+1}} - s\bar{\boldsymbol{p}}_{c_0b_{k}} &= (s\bar{\boldsymbol{p}}_{c_0c_{k+1}} - \boldsymbol{R}_{c_0b_{k+1}}\boldsymbol{p}_{bc}) - (s\bar{\boldsymbol{p}}_{c_0c_k} - \boldsymbol{R}_{c_0b_k}\boldsymbol{p}_{bc})
\end{aligned}
$$

代入上式，化简整理得：

$$
\begin{aligned}
\tilde{\boldsymbol{\alpha}}_{b_kb_{k+1}} &= s\boldsymbol{R}_{b_kc_0}(\bar{\boldsymbol{p}}_{c_0c_{k+1}} - \bar{\boldsymbol{p}}_{c_0c_{k}} ) - \boldsymbol{R}_{b_kc_0}\boldsymbol{R}_{c_0b_{k+1}}\boldsymbol{p}_{bc} + \boldsymbol{p}_{bc} + \frac{1}{2}\boldsymbol{R}_{b_kc_0}\boldsymbol{g}^{c_0}\Delta t^2 - \boldsymbol{v}^{b_k}_{b_k}\Delta t)\\
\tilde{\boldsymbol{\beta}}_{{b_k}b_{k+1}}&= \boldsymbol{R}_{b_kc_0}(\boldsymbol{R}_{c_0b_{k+1}}\boldsymbol{v}^{b_{k+1}}_{b_{k+1}} + \boldsymbol{g}^{c_0}\Delta t) - \boldsymbol{v}^{b_k}_{b_k}
\end{aligned}
$$

整理上式方程得到关于待估计变量的线性测量方程：

$$
\tilde{\boldsymbol{z}}_{b_kb_{k+1}} = \boldsymbol{H}_{b_kb_{k+1}}\boldsymbol{x}_k + \boldsymbol{n}_{b_kb_{k+1}}
$$

其中，

$$
\begin{aligned}
    \tilde{\boldsymbol{z}}_{b_kb_{k+1}} &= 
    \begin{bmatrix}
        \tilde{\boldsymbol{\alpha}}_{b_kb_{k+1}} + \boldsymbol{R}_{b_kc_0}\boldsymbol{R}_{c_0b_{k+1}}\boldsymbol{p}_{bc} - \boldsymbol{p}_{bc}\\
        \tilde{\boldsymbol{\beta}}_{{b_k}b_{k+1}}
    \end{bmatrix}\\
    \boldsymbol{H}_{b_kb_{k+1}} &= 
    \begin{bmatrix}
        -\boldsymbol{I}\Delta t & \boldsymbol{0} & \frac{1}{2}\boldsymbol{R}_{b_kc_0}\Delta t^2 & \boldsymbol{R}_{b_kc_0}(\bar{\boldsymbol{p}}_{c_0c_{k+1}} - \bar{\boldsymbol{p}}_{c_0c_{k}} )\\
        -\boldsymbol{I} & \boldsymbol{R}_{b_kc_0}\boldsymbol{R}_{c_0b_{k+1}} & \boldsymbol{R}_{b_kc_0} & \boldsymbol{0}
    \end{bmatrix}\\
    \boldsymbol{x}_k &= 
    \begin{bmatrix}
        \boldsymbol{v}^{b_k}_{b_k}\\
        \boldsymbol{v}^{b_{k+1}}_{b_{k+1}}\\
        \boldsymbol{g}^{c_0}\\
        s
    \end{bmatrix}
\end{aligned}
$$

因此，我们可以构建以下线性最小二乘问题，并应用优化的方式求解待估计状态值：

$$
\boldsymbol{x}^* = \arg\min_{\boldsymbol{x}}(\sum_i||\tilde{\boldsymbol{z}}_{b_kb_{k+1}} - \boldsymbol{H}_{b_kb_{k+1}}\boldsymbol{x}_k||^2)
$$

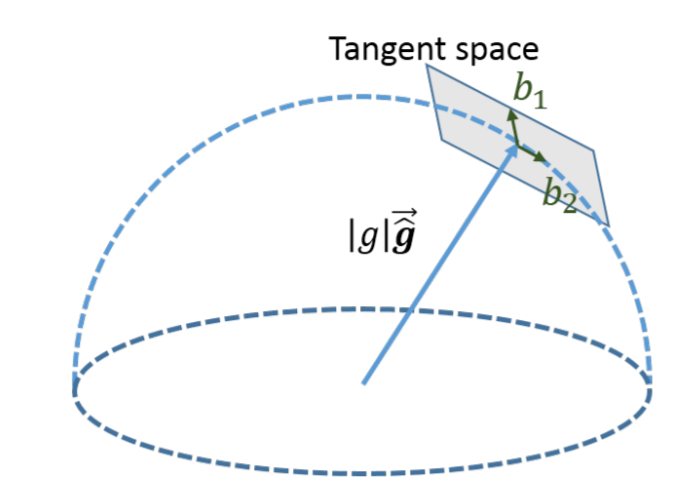
上式中，我们对 $\boldsymbol{g}^{c_0}$ 没有进行额外的限制，但实际上我们知道重力加速度的模长 $||\boldsymbol{g}^{c_0}|| = 9.81$ ，因此重力加速度实际上只有两个自由度，因此我们可以将重力进行重新参数化，使其在最小二乘问题中只有两个自由度。考虑初始时刻的相机坐标系所处的正切平面，如下图所示：

从图中可以观察看到，我们可以只用 $\boldsymbol{b}_1, \boldsymbol{b}_2$ 这两个轴对重力加速度进行参数化，如下所示：

$$
\tilde{\boldsymbol{g}}^{c_0} = ||g||\tilde{\bar{\boldsymbol{g}}}^{c_0} + w_1\boldsymbol{b}_1 + w_2\boldsymbol{b}_2
$$

其中， $w_1, w_2$ 为重力加速度在 $\boldsymbol{b}_1, \boldsymbol{b}_2$ 下的大小，也是待估计值。 $\boldsymbol{b}_1, \boldsymbol{b}_2$ 和 $\tilde{\bar{\boldsymbol{g}}}^{c_0}$ 的关系为：

$$
\begin{aligned}
    \boldsymbol{b}_1 &= \left\{
    \begin{aligned}
        \tilde{\bar{\boldsymbol{g}}}^{c_0} \times [1, 0, 0], \qquad &\tilde{\bar{\boldsymbol{g}}}^{c_0} \neq [1, 0, 0]^T\\
        \tilde{\bar{\boldsymbol{g}}}^{c_0} \times [0, 0, 1], \qquad &\text{otherwise}\\
    \end{aligned}
    \right.\\
    \boldsymbol{b}_2 &= \tilde{\bar{\boldsymbol{g}}}^{c_0} \times \boldsymbol{b}_1
\end{aligned}
$$

利用重新参数化后的重力加速度 $\tilde{\boldsymbol{g}}^{c_0} = ||g||\tilde{\bar{\boldsymbol{g}}}^{c_0} + (0, w_1, w_2)^T$ 代入观测方程中，并分离出固定量，有：

$$
\tilde{\boldsymbol{z}}_{b_kb_{k+1}} = 
\begin{bmatrix}
    \tilde{\boldsymbol{\alpha}}_{b_kb_{k+1}} + \boldsymbol{R}_{b_kc_0}\boldsymbol{R}_{c_0b_{k+1}}\boldsymbol{p}_{bc} - \boldsymbol{p}_{bc} - \frac{1}{2}\boldsymbol{R}_{b_kc_0}\Delta t^2||g||\tilde{\bar{\boldsymbol{g}}}^{c_0}\\
    \tilde{\boldsymbol{\beta}}_{{b_k}b_{k+1}} - \boldsymbol{R}_{b_kc_0}\Delta t||g||\tilde{\bar{\boldsymbol{g}}}^{c_0}
\end{bmatrix}
$$

相机坐标系对齐世界坐标系

上述过程中，我们一直以初始时刻相机坐标系作为世界坐标系，实际上我们要将世界坐标系与重力对齐，因此需要计算初始时刻相机坐标系和世界坐标系的相对旋转 $\boldsymbol{R}_{wc_0} = \exp{(\theta\boldsymbol{u})}$ ，利用使用初始相机估计出来的重力加速度和实际的重力加速度比较即可，计算方式如下：

$$
\begin{aligned}
    \boldsymbol{u} &= \frac{\tilde{\boldsymbol{g}}^{c_0}\times\tilde{\boldsymbol{g}}^w}{||\tilde{\boldsymbol{g}}^{c_0}\times\tilde{\boldsymbol{g}}^w||}\\
    \theta &= \arctan(||\tilde{\boldsymbol{g}}^{c_0}\times\tilde{\boldsymbol{g}}^w||/(\tilde{\boldsymbol{g}}^{c_0}\tilde{\boldsymbol{g}}^w))
\end{aligned}
$$

至此，VINS-MONO 中的系统初始化完成。

测量数据处理

测量数据处理作为 VINS-MONO 的前端，过程大致为：

使用LK光流追踪上一帧的特征点，估计位姿变化，具体可以参考：VIO 中的前端基本流程
计算 IMU 预积分

滑动窗口局部位姿优化

当有新的关键帧被加入至滑动窗口时，进行旧关键帧的边缘化，更新先验、视觉以及 IMU 残差进行非线性优化。具体过程可以参考我之前整理的几篇博客。

回环检测以及全局位姿图优化

思路基本同上一部分，VINS-MONO 使用 DBoW2 进行回环检车。当检测到回环时，提取出回环中涉及的所有关键帧，并进行全局非线性优化。