题目描述
题目链接:952. Largest Component Size by Common Factor
Given a non-empty array of unique positive integers A, consider the following graph:
- There are A.length nodes, labelled A[0] to A[A.length - 1];
- There is an edge between A[i] and A[j] if and only if A[i] and A[j] share a common factor greater than 1. Return the size of the largest connected component in the graph.
例子
例子 1
Input: [4,6,15,35] Output: 4 Explanation
例子 2
Input: [20,50,9,63] Output: 2 Explanation
例子 3
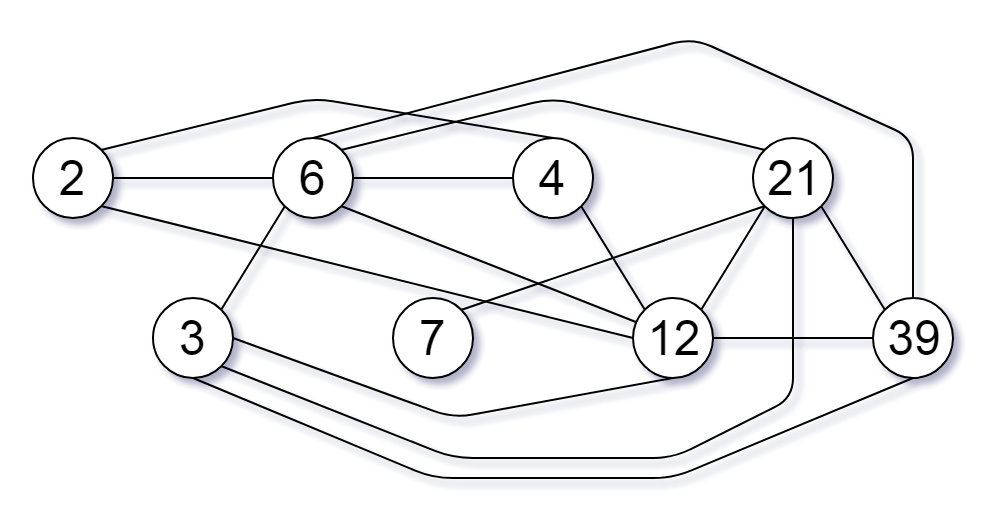
Input: [2,3,6,7,4,12,21,39] Output: 8 Explanation
Note
1 <= A.length <= 200001 <= A[i] <= 100000
解题思路
这道题主要参考了这篇博客的思路:花花酱 LeetCode 952. Largest Component Size by Common Factor 这一类查找最大的 Component 的题目一般可以想到用图的思路来完成,具体到这道题是可以通过并查集来将互相之间有联系的节点联系起来。但是通常的并查集建立操作需要两两之间互相比较,意味着时间复杂度是 O(n^2)。针对这道题的规模肯定不可行,这个时候我们注意到数组中最大元素是 100000,而我们知道一个数要查找它的因子的话最多只需要从 2 遍历到 sqrt(num)。在这道题是 sqrt(100000) ~ 300,通过这个方法我们可以想到利用每个数字的因子来作为联系的节点建立并查集,这样对于每一个数只需要操作 sqrt(num) 次。假设最大数字为 M,时间复杂度为 O(n * Sqrt(M)),空间复杂度为 O(M),最后再将所有有联系的节点联合在一起找到最大的集合即可,代码如下:
#include <vector>
#include <algorithm>
#include <unordered_map>
#include <cmath>
class DisjointSet {
public:
DisjointSet(int n) : m_parents(n) {
for (int i = 0; i < n; i++) {
m_parents[i] = i;
}
}
void Union(int x, int y) {
m_parents[Find(x)] = m_parents[Find(y)];
}
int Find(int x) {
// reset all nodes with same parents
if (m_parents[x] != x) {
m_parents[x] = Find(m_parents[x]);
}
return m_parents[x];
}
private:
std::vector<int> m_parents;
};
class Solution {
public:
int largestComponentSize(std::vector<int>& A) {
int n = *std::max_element(A.begin(), A.end());
DisjointSet ds(n + 1);
for (int a: A) {
for (int factor = 2; factor <= std::sqrt(a); factor++) {
if (a % factor == 0) {
ds.Union(a, factor);
ds.Union(a, a / factor);
}
}
}
std::unordered_map<int, int> count; // component size for all parents
int max_size = 1;
for (int a : A) {
max_size = std::max(max_size, ++count[ds.Find(a)]);
}
return max_size;
}
};
- 时间复杂度: O(n * sqrt(M))
- 空间复杂度: O(M)