本文是我在学习深蓝学院的激光slam课程第五次实践的笔记。本次作业主要是熟悉高斯牛顿法进行点云配准的代码实现。
实现高斯牛顿法进行点云配准
补充代码,实现 gaussian_newton_scanmatcher 模块
代码结构
老规矩,还是先阅读给定的框架代码,了解代码结构再考虑补全。这次作业主要也是涉及两个源文件,分别是 main.cpp 和 gaussian_newton_method.cpp。其中,main.cpp 里包含了一个 GaussianNewtonDebug 类,完成了 ROS 的相关设置,包括订阅和发布消息,消息的类型转换(将订阅的激光扫描话题消息转为更加方便使用的 vector),以及调用 gaussian_new_method.cpp 里定义的关于高斯牛顿法的相关函数。除了这两个文件之外,还提供了 map.c 和 map_cspace.cpp 两个文件,主要是外部提供的一些关于地图的模块。下面重点讲一下 gaussian_new_method.cpp
高斯牛顿法相关代码
gaussian_new_method.cpp 主要提供了关于高斯牛顿法的几个函数,有几个比较简单就不说了,对要补充的三个函数下面进行介绍。
Eigen::Vector3d InterpMapValueWithDerivatives(map_t* map,Eigen::Vector2d& coords):通过周围四个已知点插值计算出指定坐标点的势场值和梯度,这里可以用课程中提到的拉格朗日双方向插值来进行计算。注意计算出来的梯度需要考虑到尺度的影响。补充代码如下:
Eigen::Vector3d InterpMapValueWithDerivatives(map_t* map,Eigen::Vector2d& coords)
{
Eigen::Vector3d ans;
/// calculate coordinates on the given map (noticed: might not be exact interger)
/// remember the origin of map locates in center of the map thus need to plus half of size to get the real index
double index_x = (coords(0) - map->origin_x) / map->resolution + map->size_x / 2;
double index_y = (coords(1) - map->origin_y) / map->resolution + map->size_y / 2;
int16_t index_x0 = floor(index_x);
int16_t index_y0 = floor(index_y);
/// calculate u, v using four nearest points
double u, v;
u = index_x - index_x0;
v = index_y - index_y0;
/// calcualte scores for four nearest points
double z1 = map->cells[MAP_INDEX(map, index_x0, index_y0)].score;
double z2 = map->cells[MAP_INDEX(map, index_x0 + 1, index_y0)].score;
double z3 = map->cells[MAP_INDEX(map, index_x0 + 1, index_y0 + 1)].score;
double z4 = map->cells[MAP_INDEX(map, index_x0, index_y0 + 1)].score;
/// score of given coordinate in the map
ans(0) = (1 - u) * (1 - v) * z1 + u * (1 - v) * z2 + u * v * z3 + (1 - u) * v *z4;
/// gradient
/// noticed: need to remove scale influence by using resolution
ans(1) = (v * (z3 - z4) + (1 - v) * (z2 - z1)) / map->resolution;
ans(2) = (u * (z3 - z2) + (1 - u) * (z4 - z1)) / map->resolution;
return ans;
}
void ComputeHessianAndb(map_t* map, Eigen::Vector3d now_pose,std::vector<Eigen::Vector2d>& laser_pts,Eigen::Matrix3d& H, Eigen::Vector3d& b): 计算 H 和 b 用来进行高斯优化,这里通过笔记中的方法计算即可,需要注意的是激光点和机器人的相对以及绝对 pose 的关系,不要用混,以及 J 矩阵的维度:
void ComputeHessianAndb(map_t* map, Eigen::Vector3d now_pose,
std::vector<Eigen::Vector2d>& laser_pts,
Eigen::Matrix3d& H, Eigen::Vector3d& b)
{
H = Eigen::Matrix3d::Zero();
b = Eigen::Vector3d::Zero();
for (Eigen::Vector2d pt: laser_pts) {
/// compute laser pt pose globally
Eigen::Vector2d pt_pose = GN_TransPoint(pt, now_pose);
Eigen::Matrix<double, 2, 3> ds;
ds << 1, 0, -sin(now_pose(2) * pt(0)) - cos(now_pose(2)) * pt(1),
0, 1, cos(now_pose(2) * pt(0)) - sin(now_pose(2)) * pt(1);
/// compute score & grident of that point in map
Eigen::Vector3d score_gradient = InterpMapValueWithDerivatives(map, pt_pose);
Eigen::Vector2d gradient(score_gradient(1), score_gradient(2));
double score = score_gradient(0);
/// noticed the dimension of J should 1 x 3
Eigen::RowVector3d J = gradient.transpose() * ds;
H += J.transpose() * J;
b += J.transpose() * (1 - score);
}
}
void GaussianNewtonOptimization(map_t*map,Eigen::Vector3d& init_pose,std::vector<Eigen::Vector2d>& laser_pts): 进行高斯优化,这一部分按照常规操作即可
void GaussianNewtonOptimization(map_t*map,Eigen::Vector3d& init_pose,std::vector<Eigen::Vector2d>& laser_pts)
{
int maxIteration = 20;
Eigen::Vector3d now_pose = init_pose;
Eigen::Matrix3d H;
Eigen::Vector3d b;
for(int i = 0; i < maxIteration;i++)
{
ComputeHessianAndb(map, now_pose, laser_pts, H, b);
Eigen::Vector3d delta_x = H.colPivHouseholderQr().solve(b);
now_pose += delta_x;
}
init_pose = now_pose;
}
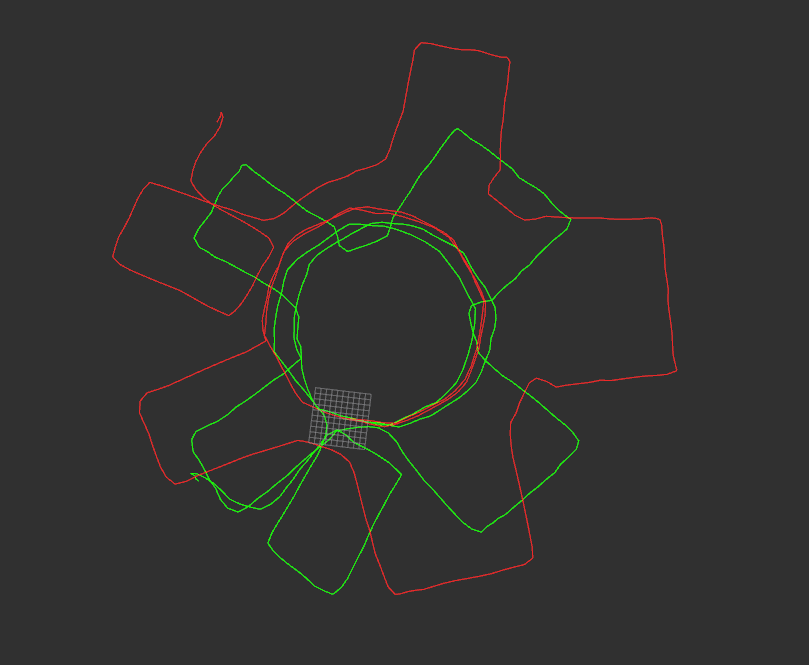
运行结果
运行结果如下图所示:
可以看出基本轮廓比较符合,但由于每一步的误差导致最后偏离较远,需要后端来进行校正。同时通过调整迭代次数和迭代终止条件也能进一步对算法效果进行微调。
对上一题算法进行改进的方案
提出一种能提升第一题激光匹配轨迹精度的方法,并解释原因
除了调整迭代次数以外,还可以:
- 使用另一种算法进行迭代,比如 LM 算法
- 对点云进行预处理,进行运动畸变的去除,过滤噪声等
- 使用更多点进行插值
NDT相关
读论文 The Normal Distributions Transform: A New Approach to Laser Scan Matching,回 答以下问题 NDT 的优化函数(score)是什么? 简述 NDT 根据 score 函数进行优化求解的过程。
参考我的上一篇笔记:激光SLAM 前端配准方法 - 基于势场的方法
分支定界相关
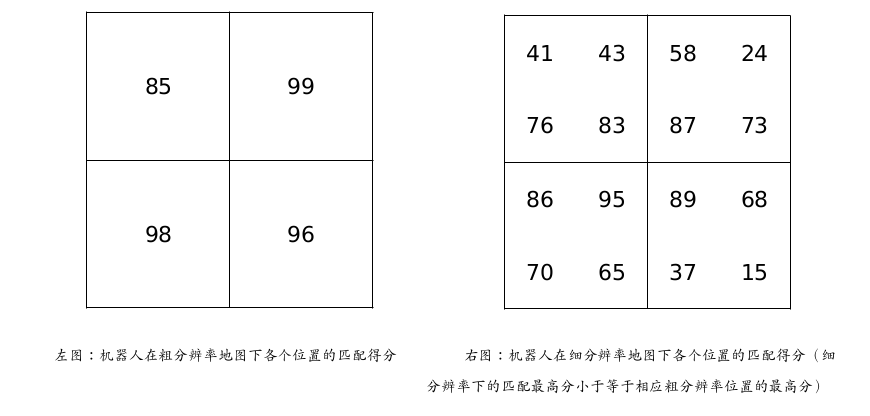
机器人在 XY 方向上进行 CSM 匹配。下图左为机器人在目标区域粗分辨率下 4 个位置的匹配得分,得 分越高说明机器人在该位置匹配的越好,下图右为机器人在同一块地图细分辨率下每个位置的匹配得分(右 图左上 4 个小格对应左图左上一个大格,其它同理)。如果利用分枝定界方法获取最终细分辨率下机器人 的最佳匹配位置,请简述匹配和剪枝流程。
首先将粗分辨率的四个节点分别定为 0, 1, 2, 3,细分辨率节点命名类似;
首先进行第一次计算:找出粗分辨率下分数最高的节点,选出 1 节点 (99分) 进行分支; 对 1 节点进行分支获得四个分数;最高分为 12 节点 (87分),并且该分支已经是子节点(所需要的分辨率),所以可以用该分数作为阈值进行剪枝;因此 0 节点不需要考虑; 接下来对 2 节点分支,最高分为 21 节点 (95分),因此更新最高分为 95 分; 最后对 3 节点分支,最高分为 89 分,不影响结果。 因此最后取 21 节点作为解,分数为 95 分。